NP-Completeness

內容目錄

Cook-Levin Theorem

首先需要一個問題叫做布林公式(Boolean formula)會像：

$\phi = (\bar{x} \wedge y) \vee (x \wedge \bar{z})$

裡面的每一個符號稱作variable，每一個variable可以給0或1的值就像在做布林運算，一個boolean formula要滿足的話要讓各個variable做完計算後 $\phi$ 輸出1
而有一種問題叫做satisfiability problem就是倚靠boolean formula是否滿足來達成條件

$SAT = \{<\phi>| \phi \> is \> a \>satisfiable \> Boolean \> formula\}$

定理：Cook-Levin Theorem

$SAT \in P \>\> iff \>\> P = NP$

定義：
$f: \Sigma^{*} \rightarrow \Sigma^{*}$ 如果存在多項式時間的Turing Machine M可以接受任何輸入w，並且在tape裡 $f(\omega)$ 步驟之後停止並且輸出結果就稱這是一個多項式時間可運算的function
定義：
如果存在一個多項式時間可計算的function $f: \Sigma^{*} \rightarrow \Sigma^{*}$ ， $f$ 能輸入任何字串 $\omega$ ，代表可以讓language A在多項式時間內映射(mapping)轉換(reducible)到language B上，可以表示成 $A \leq_{p} B$ 或者可以表示成以下的對應函數：

$\omega \in A \Leftrightarrow f(\omega) \in B$

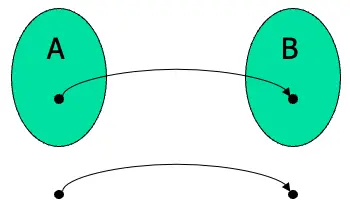
這個function $f$ 做的事情是讓問題A在多項式時間內轉換到問題B
定義：如果 $A \leq_{p} B$ 並且 $B \in P$ , 則代表 $A \in P$
證明：
存在一組多項式時間Turing Machine M可以決定B的結果並且 $f$ 作為多項式時間轉換將A問題換成B問題
N = 輸入任何字串 $\omega$

計算 $f(\omega)$
放進輸入執行M並且不管M有沒有輸出 $f(\omega)$ 都一定要輸出一個結果(這樣才符合algorithm的定義)
定義：
如果一個language B滿足以下兩個條件就可以稱作NP-complete
(1) 問題B屬於NP
(2) 任何問題A屬於NP並且在多項式時間轉換到問題B
(如果只有條件(2)滿足的話叫做NP-hard的特性)
定理：如果B是NP-complete並且 $B \in P$ ，那麼 $P = NP$
證明：參照多項式時間轉換的定義
定義：如果B是NP-complete並且 $B \leq_{p} C$ 對於 $C \in NP$ ，那麼C也會是NP-complete
證明：存在任何的language $A \in NP$ 能夠在多項式時間內轉換到 $C$
$\because B$ 是NP-complete, $\therefore$ 任何的language $\in NP$ 都可以在多項式時間內轉換到B

$A \leq_{p}B, B \leq_{p} C \Rightarrow A \leq_{p} C$

至此所有的language屬於NP都可以在多項式時間內轉換到C
定義：
literal: 一個boolean variable或是一個negated boolean(variable $x$ 或者 $\bar{x}$ )
clause: $(x_{1} \vee \bar{v_{2}} \vee x_{3} \vee \bar{x_{4}})$
conjunctive normal form (CNF):

$(x_{1} \vee x_{2} \vee \bar{x_{3}}) \wedge (x_{4} \vee \bar{x_{5}}) \wedge (x_{3} \vee \bar{x_{6}})$

3CNF-formula:

$(x_{1} \vee x_{2} \vee \bar{x_{3}}) \wedge (x_{3} \vee \bar{x_{5}} \vee x_{6}) \wedge (x_{3} \vee \bar{x_{6}} \vee x_{4})$

3SAT = $\{<\phi>|\phi$ 是一個satisfiable 3cnf-formula $\}$
定理：3SAT可以在多項式時間內轉換到CLIQUE
證明：讓 $\phi$ 作為一個formula擁有 $k$ 個clauses:

$\phi = (a_{1} \vee b_{1} \vee c_{1}) \wedge (a_{2} \vee b_{2} \vee c_{2}) \wedge … \wedge(a_{k} \vee b_{k} \vee c_{k}) \underset{\Longrightarrow}{f} <G, k>$

$\phi = (x_{1} \vee x_{1} \vee x_{2}) \wedge (\bar{x_{1}} \vee \bar{x_{2}} \vee \bar{x_{2}}) \wedge (\bar{x_{1}} \vee x_{2} \vee x_{2})$

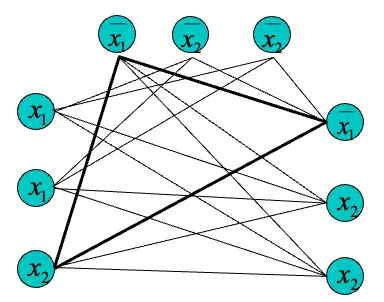
其中 $f$ 為多項式時間的轉換function
而 $\phi$ 要能夠滿足的話若且唯若 $\in CLIQUE$

Cook-Levin Theorem

$SAT \in NP-complete$
證明：

- 一個NTM可以猜formula的variable並且在驗證過後看是否滿足 $\phi$
對於任何的並且A可以在多項式時間內轉換到SAT問題上
- 假設N是一個Non-deterministic Turing Machine可以在 $n^{k}$ 時間內決定A的輸出， $k \in constant$ ，NTM N存在一組表輸入w制定出 $n^{k} \times n^{k}$ 大小的表，每一列是NTM的每一條分支在計算輸入w的configuration，如果任何一列結果是accepting的configuration就代表整個表輸出就是accepting

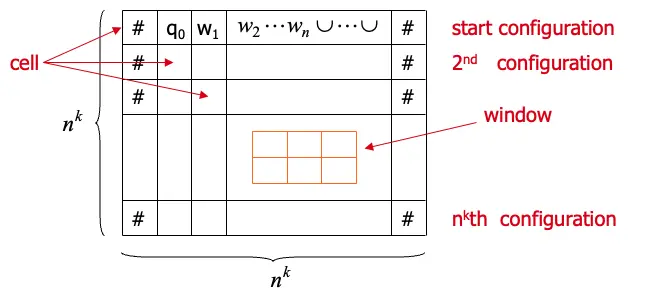
任何accepting的表都是跟NTM N輸入w字串計算後的分支有關

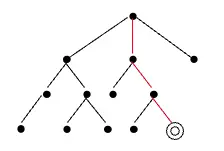
NTM N能夠accept輸入w就代表存在accepting表能決定輸出結果是accept或是reject

$f:$ 多項式時間轉換問題A到SAT問題
輸入w作為問題A的instance，將w轉換產生成formula $\phi$
假設 $Q$ 跟 $\Gamma$ 作為N的state集合以及tape的alphabet
讓 $C = Q \cup \Gamma \cup {#}$ 從 $1 \leq i, j \leq n^{k}$ 以及每一個 $s \in C$ ，可以產生 $x_{i, j, s} \thicksim n^{2k}$ 個variable
如果 $x_{i, j, s} = 1$ 代表cell[i, j]包含 $s$
設計一組 $\phi$ 可以滿足variable與NTM N輸入w的結果產生一組accepting表

$\phi = \phi_{cell} \wedge \phi_{start} \wedge \phi_{move} \wedge \phi_{accept}$

(1)

$\phi_{cell} = \underset{i \leq i, j \leq n^{k}}{\vee}[(\underset{s \in C}{\vee}x_{i,j,s}) \wedge (\underset{s, t \in C, s \neq t}{\wedge} (\bar{x_{i,j,s}} \vee \bar{x_{i,j,t}}))]$

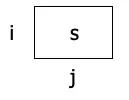
(2)

$\phi_{start} = x_{1,1,#} \wedge x_{1,2,q_{0}} \wedge x_{1,3,w_{1}} \wedge x_{1, 4,w_{2}} \wedge … \wedge x_{1,n+2,w_{n}} \wedge x_{1,n+3,\cup} \wedge … \wedge x_{x_{1},n^{k}-1, \cup} \wedge x_{1, n^{k}, #}$

要確認的是第一個row是NTM N輸入w的start configuration，以上就完成表內的一行row，還要再另外產生 $n^{k}-1$ 組row
(3) $\phi_{accept}$ 保證表內一定會產生一組accepting的configuration

$\phi_{accept} = \underset{1 \leq i, j \leq n^{k}}{\vee} x_{i,j,q_{accept}}$

(4) $\phi_{move}$ ：
保證表裡面的每一個row都可以合法地透過NTM N的transition rule來產生
$\delta(q_{1},a) = {q_{1}, b, R}$
$\delta(q_{1},b) = {(q_{2}, c, L), (q_{2}, a, R)}$
$\delta(q_{2}, a) = {q_{2}, b, R}$

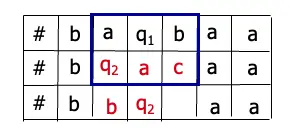
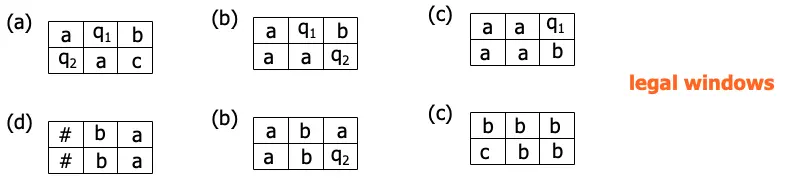
合法範例

Claim: 首先檢查第一層的row是不是start configuration，如果是的話代表接下來表內的內容都是合法的，並且上一層跟下一層的configuration都要遵照transition rule

$\phi_{move} = \underset{1 \leq i, j \leq n^{k}}{\vee}$ ( $i, j$ 的表格內容必須是合法的) =

$\underset{a_{1},….,a_{6}}{\vee}(x_{i-1,j,a_{1}} \wedge x_{i,j,a_{2}} \wedge x_{i+1,j,a_{3}} \wedge x_{i-1, j+1, a_{4}} \wedge x_{i,j+1,a_{5}} \wedge x_{i+1,j+1,a_{6}})$

需要一次看六格是不是合法的

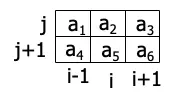
$\phi$ 的大小是 $O(n^{2k})$ ，讓 $|C| = l \thicksim$ 依據N設計的transition大小
總共所有variable會有 $O(n^{2k})$
$\phi_{cell}:O(n^{2k}), \phi_{start}:O(n^{k})$
$\phi_{accept}, \phi_{move}: O(n^{2k})$ 因此轉換可以在多項式時間內完成

推論(Cor)：3SAT是NP-complete

證明：3SAT屬於NP
$SAT \leq_{p} 3SAT$
$(a_{1} \vee a_{2} \vee a_{3} \vee a_{4}) \equiv (a_{1} \vee a_{2} \vee z) \wedge (\bar{z} \vee a_{3} \vee a_{4})$
如果 $l > 3, (a_{1} \vee a_{2} \vee a_{3} \vee …. \vee a_{l})$

$\equiv (a_{1} \vee a_{2} \vee z_{1}) \wedge (\bar{z_{1}} \vee a_{3} \vee a_{2}) \wedge (\bar{z_{2}} \vee a_{4} \vee z_{3}) \wedge … \wedge (\bar{z_{l-3}} \vee a_{l-1} \vee a_{l})$

推論(Cor)：CLIQUE屬於NP-complete

圖G的頂點覆蓋(Vertex cover of G)：如果G屬於一個無向圖，G裡覆蓋的頂點(Vertex cover)是圖G裡一個子集合能夠讓G的每一條邊都接著一個點

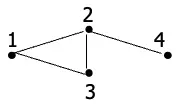
$\{2, 3\}$ 是一組vertex cover
$\{1, 3\}$ 不是一組vertex cover
Vertex-Cover = { $<G, k>$ |G是一個無向圖並且擁有k個點的vertex cover}
定理：Vertex-Cover屬於NP-complete
證明：Vertex-Cover屬於NP

$3SAT \leq_{p} VERTEX-COVER$

$\phi = (x_{1} \vee x_{1} \vee x_{2}) \wedge (\bar{x_{1}} \vee \bar{x_{2}} \vee \bar{x_{2}}) \wedge (\bar{x_{1}} \vee x_{2} \vee x_{2})$

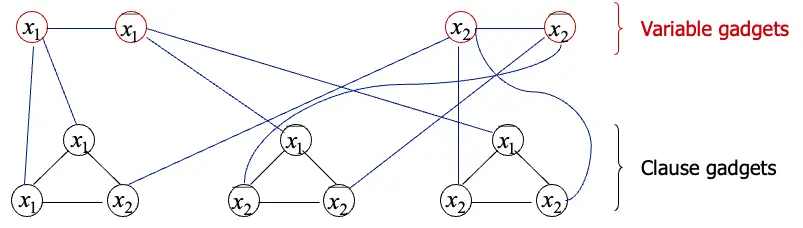
靠以上的轉換方法來證明滿足 $\phi$ 的話代表G確實存在k個node的vertex cover
讓 $\phi$ 擁有 $m$ 個variable以及 $l$ 個clauses使得 $k = m+2l$

另外設計gadgets作為輔助的元件，一個true variable來自每個variable gadgets，兩個node來自clause gadget
每三個邊可以連接variable gadgets跟clause gadget來覆蓋

SUBSET-SUM

SUBSET-SUM = { $<S, t>|S = \{x_{1},…,x_{k}\}$ 以及對於某些 $\{y_{1},…,y_{i}} \subseteq S, \sum_{y_{i}} = t$ }
定理：SUBSET-SUM屬於NP-complete
證明：SUBSET-SUM屬於NP

$3SAT \leq_{p} SUBSET-SUM$

存在 $\phi$ 是一個boolean formula擁有variables $x_{1},…,x_{i}$ 以及clauses $c_{1},….,c_{k}$

$\phi = c_{1} \wedge c_{2} \wedge …. \wedge c_{k}|\phi \rightarrow\ <S, t>$

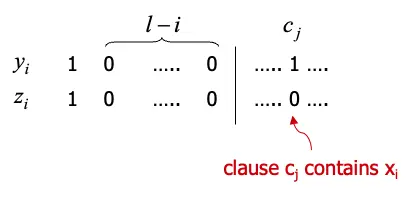
假設 $\phi$ 滿足的話，建構一個子集合 $S$ ，如果 $x_{i}$ 給的值是TRUE，選擇 $y_{i}$ ，否則就另外選擇 $z_{i}$ ，對於每一次的i，一次只會選擇 $y_{i}$ 或 $z_{i}$ 代表true或false，最後k個digits會把整個 $i$ 加總起來算1，如果不到3的話由 $g$ 跟 $h$ 來補到3

假設一組S的子集合可以加總到 $t$ ，可以建構一組滿足 $\phi$ 的公式，如果這組子集合包含 $y_{i}$ 我們就設定 $x_{i}$ 為TRUE，否則設定 $x_{i}$ 為FALSE，而這樣的條件可以滿足 $\phi$
整張表的大小是 $O((k+i)^{2}) \thicksim O(n^{2})$

定理： $HAMPATH \in NP-complete$

$3SAT \leq_{p} HAMPATH$

證明：存在一組3cnf-formula擁有k個clauses

$\phi = (a_{1} \vee b_{1} \vee c_{1}) \wedge (a_{2} \vee b_{2} \vee c_{2}) \wedge … \wedge (a_{k} \vee b_{k} \vee c_{k})$

每一個 $a,b,c$ 可以看作literal的 $x_{i}$ 或者 $\bar{x_{i}}$ 以及 $x_{1},…..,x_{i}$ 都是 $\phi$ 的variables

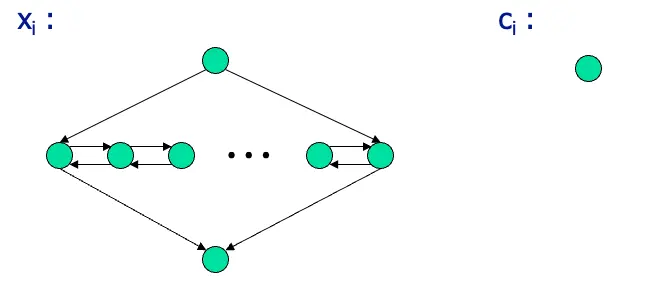
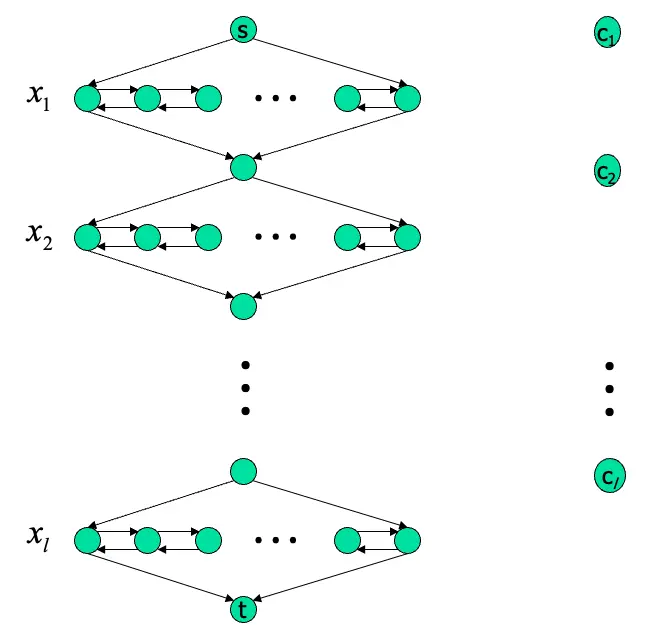
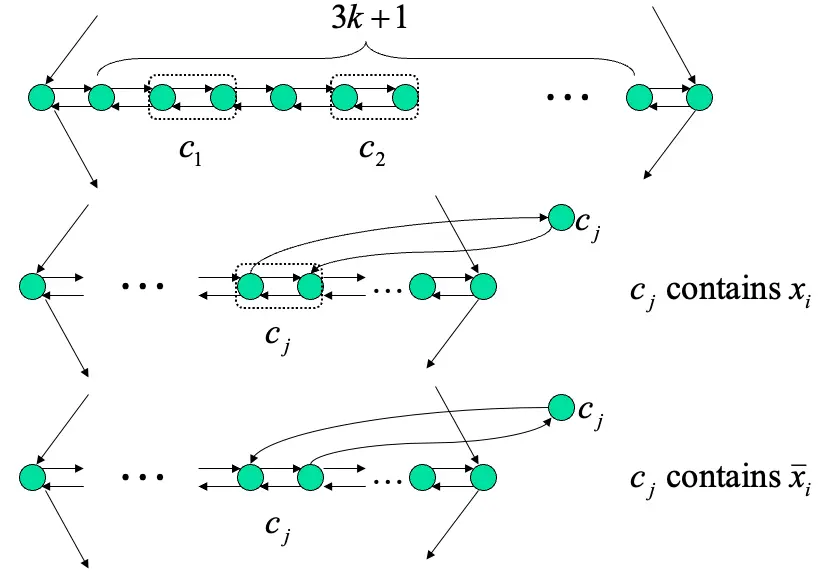
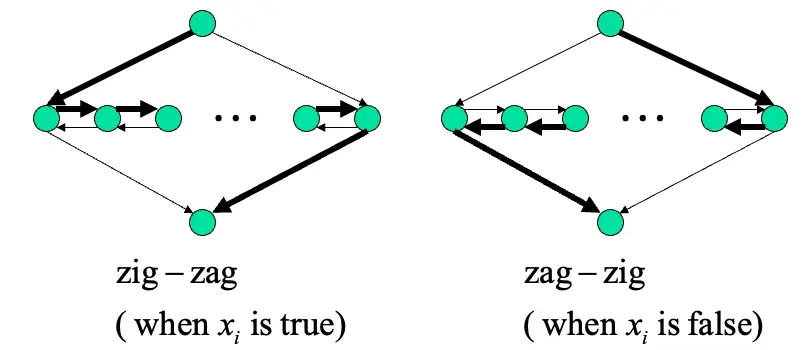
如果存在一組可以滿足的參數，選擇clause裡面其中一個literal給TRUE
如果存在可以得到true的結果，代表存在一組Hamiltonian path從 $s$ 走到 $t$
如果Hamiltonian path是 $normal$ ，意思是可以從上面的鑽石型路徑頂端node走到最尾端的node，代表可以輕鬆找到一組滿足3CNF的路徑，因為每一組clause的點出現在路徑裡，只要點存在並且給TRUE的值，就可以接著走下去，如果是走 $zig-zag$ 路徑就讓每一個node放TRUE，反之走 $zag-zig$ 每一個點給False。
而Hamiltonian path必須是 $normal$ 的

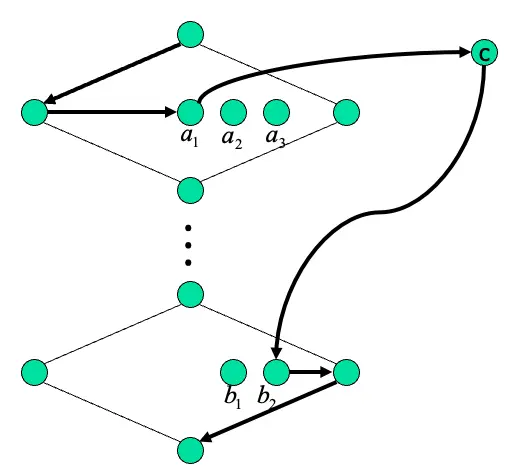
假設有兩種case:
case 1: $a_{2}$ 是一個離群的點
case 2: $a_{3}$ 是一個離群的點
在兩種情況下，路徑不包含 $a_{2}$ 的點
在case 1: 路徑沒辦法從 $a_{1}$ 或者 $c$ 進入，因為路徑走到了其他的點上
在case 2: 路徑沒辦法從 $a_{3}$ 進入，因為 $a_{3}$ 跟 $a_{2}$ 一樣是獨立的node在此種情況

定理：UHAMPATH屬於NP-complete

證明：

$HAMPATH \leq_{p} UHAMPATH$

$Directed \> Graph \> G \rightarrow Undirected \> Graph \> G'$

$u \in V(G)$
$G'$ 的點: $u \Rightarrow u^{in}, u^{mid}, u^{out}$
$s \Rightarrow s^{out}, t \Rightarrow t^{in}$
$G'$ 的邊: $u \rightarrow v \in E(G) \Rightarrow u^{in} - u^{mid} - u^{out} - v^{in} - v^{mid} - v^{out}$

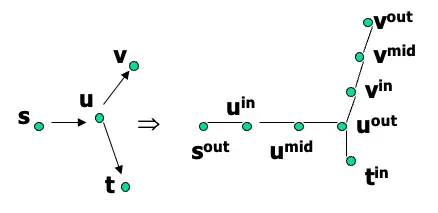
如果 $s \rightarrow u_{1} \rightarrow u_{2} \rightarrow … \rightarrow u_{k} \rightarrow t$ 是 $G$ 裡的Hamiltonian path
則 $s^{out} - u^{in}_{1} - u^{mid}_{1} - u^{out}_{1} - u^{in}_{2} - u^{mid}_{2} - u^{out}_{2} - … - u^{in}_{k} - u^{mid}_{k} - u^{out}_{k} - t^{in}$ 屬於 $G'$ 裡的無向Hamiltonian path。

Scientia Potentia Est

Scientia Potentia Est

NP-Completeness

內容目錄

Cook-Levin Theorem