圖靈機

目錄

• 有限自動狀態機與圖靈機的差異
• 範例
• Definition of Turing Machine
• Halting Configurations
  • 定義1
  • 定義2
• 範例

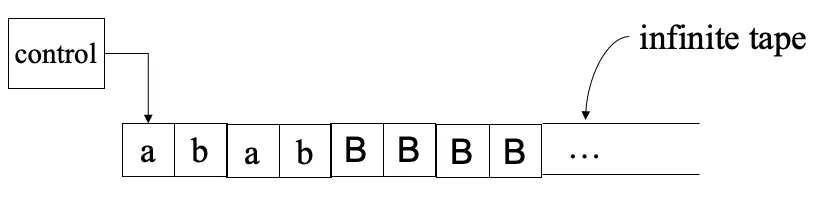
其中可以看到儲存的空間稱作tape，在Turing的概念裡這個儲存空間是無限的，裡面可以存放像是a, b這字元，另外定義B是blank的符號代表空字元，而有一個控制器的元件可以對tape裡面的位置進行讀與寫，控制器決定現在讀寫的位置，能夠進行往左一格或往右一格的移動操作，這就是最早的計算機概念，但時至今日還是以這個概念為根源，就算是平行計算，也只需要多幾組tape跟control，以及多一點的符號來紀錄讀寫位置就可以實現。

有限自動狀態機與圖靈機的差異

1. 圖靈機可以讀跟寫進tape裡
2. 控制器的讀寫頭可以往左或往右移動
3. tape的空間是無限的
4. 有多兩個特殊的state叫做accept state跟reject state

範例

假設有一個Turing Machine $M_{1}$測試能不能接受一個Language B = {w#w: $w \in {0, 1}^{*}$}，這是一個做字串比對的Language，#代表區隔兩個不同字串，如果沒有讀到#就直接reject掉。

箭頭代表目前控制器的讀寫頭位置，首先我們讀進左邊第一個位置內容是一個0，用一個符號覆寫上去代表我們已經讀過了，接著往右移找到#，在讀取#右邊找第一個0，如果找到的話我們也用一個X來覆寫上去，就這樣來來回回檢查每一個同位置的符號，如果存在一個位置的符號不一樣的話就reject掉這個字串，掃瞄完到#左右邊如果有一邊還留有原先的符號代表兩個字串長度不同就reject掉，最後如果上面的都沒有被reject掉就accept，代表兩個字串是相同的。

Definition of Turing Machine

一個Turing Machine擁有7-tuple($Q, \Sigma, \Gamma, S, q_{0}, q_{accept}, q_{reject}$), 其中$Q, \Sigma, \Gamma$屬於有限集合

1. Q: 狀態集合(包含$q_{0}, q_{1}, …, etc$)
2. $\Sigma$: 所有輸入的字母但不包含特殊符號B
3. $\Gamma$: tape的字母集合，其中{B}$\in \Gamma$並且$\Sigma \subseteq \Gamma$
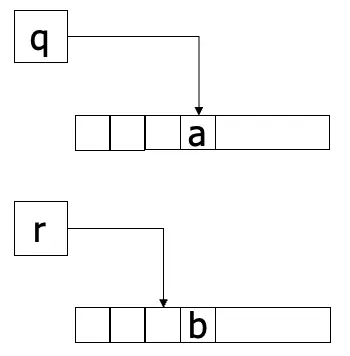
4. $\delta:Q \times \Gamma \rightarrow Q \times \Gamma \times {L, R}$ ~ transition function: $\delta (q, a) = (r, b, L)$，L是Left讀寫頭往左，而R就是Right讀寫頭往右如下圖

5. $q_{0} \in Q$: 是起始的狀態

6. $q_{accept} \in Q$: 是Turing Machine接受輸入的狀態

7. $q_{reject} \in Q$: 是Turing Machine拒絕輸入的狀態，而$q_{reject} \neq q_{accept}$

一個Turing Machine輸入字串後開始執行，最終會輸出accept或reject，也有可能永遠不會停止計算
在每一次計算中會改變

1. 現在的狀態
2. 現在Turing Machine tape的內容
3. 現在讀寫頭的位置

以上三點稱作Turing Machine的”configuration”
假設 $uqv$ 是一個configuration，$q$是目前的state，$uv$是目前tape裡面的內容，而$v$則是讀寫頭目前的位置，假設$C_{1}, C_{2}$是兩個configuration，我們說$C_{1}$得出(yields)$C_{2}$代表Turing Machine裡面存在合法的transition function讓$C_{1}$在一次計算過後變成$C_{2}$
$uaq_{i}bv$ yields $uq_{j}acv$ if $\delta(q_{i}, b) = (q_{j}, c, L)$, where $a, b \in \Gamma, u,v \in \Gamma^{*}$

反之亦然，也可以讓state看到某個符號後往右移一格，$uaq_{i}bv$ yields $uacq_{j}v$ if $\delta(q_{i}, b) = (q_{j}, c, R)$, where $a, b \in \Gamma, u,v \in \Gamma^{*}$
但要注意的是沒辦法讓讀寫頭移出到tape之外，代表不存在一個configuration $uaq_{i}B$，B符號通常是Blank的意思，代表字串的結尾
而起始的configuration可以看成 $q_{0}w$
如果Turing Machine接受輸入字串是合法的最後會變成$q_{accept}$的configuration
反之亦然，如果字串不是合法的狀態就變成$q_{reject}$

Halting Configurations

一個Turing Machine M接受輸入字串 w 如果存在一組configuration的順序是$C_{1},C_{2},…,C_{k}$以及以下的條件

1. $C_{1}$是M接收w字串後的起始configuration
2. 每一個$C_{i}$都可以得出(yields) $C_{i+1}$
3. $C_{k}$是accepting configuration

就可以稱這個字串w對於Turing Machine M來說是合法的內容，而將這些合法的字串搜集起來就代表是M的language，表示成L(M)

所以可以更嚴謹的來定義一下Turing Machine：

定義1

一個language可以被Turing Machine給識別(recognizes 或是 recursively enumerable)的話可以稱這個language是Turing-recognizable，意思是如果Turing Machine存在合法的transition rules可以產出language所有的規則就可以進入到accept的狀態，但如果被拒絕的話無法分辨是不存在還是進入到無窮執行了。

定義2

一個language可以被Turing Machine給決定(decides 或是 recursive)的話稱這個language是Turing-decidable，意思是這些language可以被Turing Machine決定接受或者如果沒出現合法的transition rule可以得出language則明確的拒絕。

範例

使用$\Sigma = {a, b}$，設計一個Turing Machine M可以accept $L = {a^{n}b^{n}: n \geq 1}$
$Q = {q_{0}, q_{1}, q_{2}, q_{3}, q_{4}}$
$\Sigma = {a, b}$
$\Gamma = {a, b, x, y, B}$
$q_{0}$: start state
$q_{4}$: accept state
$\delta(q_{0}, a) = (q_{1}, x, R)$;
$\delta(q_{1}, a) = (q_{1}, a, R)$;
$\delta(q_{1}, y) = (q_{1}, y, R)$;
$\delta(q_{1}, b) = (q_{2}, y, L)$;
$\delta(q_{2}, y) = (q_{2}, y, L)$;
$\delta(q_{2}, a) = (q_{2}, a, L)$;
$\delta(q_{2}, x) = (q_{0}, x, R)$;
$\delta(q_{0}, y) = (q_{3}, y, R)$;
$\delta(q_{3}, y) = (q_{3}, y, R)$;
$\delta(q_{3}, B) = (q_{4}, B, R)$;
$q_{0}aabb \vdash xq_{1}abb \vdash xaq_{1}bb \vdash xq_{2}ayb \vdash q_{2}xayb \vdash xq_{0}ayb \vdash xxq_{1}yb \vdash xxyq_{1}b \vdash xxq_{2}yy \vdash xq_{2}xyy \vdash xxq_{0}yy \vdash xxyq_{3}y \vdash xxyyq_{3}B \vdash xxyyBq_{4}$
M accept language $L = {a^{n}b^{n}: n \geq 1}$