目錄
測量複雜度
- Worst-case analysis
- Average-case analysis
定義一個M是Deterministic Turing Machine並且會根據輸入決定停止
- 規範M的執行時間或者時間複雜度可以表示成一個function \(f:N \rightarrow N\),其中\(f(n)\)是指M輸入長度n的最大步驟數量
- 如果\(f(n)\)是M的執行時間,可以表示M執行\(f(n)\)的時間並且稱M是一個\(f(n)\)時間的Turing Machine
Big-O以及Small-o漸進符號
定義:\(f(n) = O(g(n))\),如果存在一個正整數c(通常是個常數)以及\(n_{0}\)使得任何的\(n \geq n_{0}, f(n) \leq cg(n)\)
範例:\(f(n) = 5n^{3}+2n^{2}+22n+6\), \(f(n) = O(n^{4}), f(n) = O(n^{3})\)
顧名思義就是存在一組時間複雜度是目前$f(n)$的執行時間上限
定義:\(f, g: N \rightarrow R^{+}\), 表示\(f(n) = o(g(n))\) if \[ \underset{n \rightarrow \infty}{\operatorname{lim}}\frac{f(n)}{g(n)} = 0 \]
範例:\(\sqrt{n} = o(n), n^{2} = o(n^{3}), nloglogn = o(nlogn)\)
定義:\(t: N \rightarrow N\)作為一個function
\(TIME(t(n))\): 時間複雜度類別 = {L | L是一個language可以被\(O(t(n))\)時間的Turing Machine給決定}
不同的模型設計之下會有不同的複雜度關聯
定理:\(t(n):\)一個function \(\geq n\),任何\(t(n)\)時間的Multi-tape Turing Machine等同於\(O(t^{2}(n)\)時間的單一tape Turing Machine
定理:\(t(n):\)一個function \(\geq n\),任何\(t(n)\)時間的Non-deterministic single-tape Turing Machine等同於\(2^{O(t(n))}\)時間的deterministic single-tape Turing Machine
P類別
P是指language的類別能夠被deterministic single-tape Turing Machine在多項式時間(polynomial time)內被決定(decidable),換言之可以表示成:
\[ P = \bigcup_{k}TIME(n^{k}) \]
舉例來說:
有一組\(PATH\) = {<\(G, s, t\)>|\(G\)是一個有向圖其中存在一條有向路徑可以從\(s\)到達\(t\)}
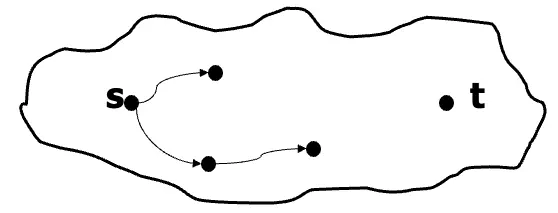
定義:\(PATH \in P\)
另外像是 \(RELPRIME\) = {<\(x, y\)>|\(x, y\)為互質},也同樣定理:\(RELPRIME \in P\)
NP類別
Hamiltonian path是一組有向圖\(G\)存在一條有向路徑可以從\(s\)走到\(t\)且每個點只經過一次
\(HAMPATH\) = {<\(G, s, t\)>|G是一個有向圖存在一條Hamiltonian path從\(s\)到\(t\)}
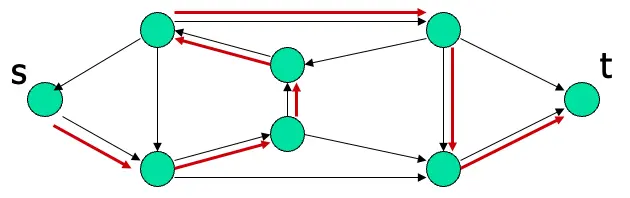
可以觀察到存在指數時間(exponential time)的演算法來解決HAMPATH問題,而要驗證HAMPATH問題的話只要給路徑的點跟線就可以在多項式時間裡驗證
\(COMPOSITES\) = {\(x| x = pq\), 對於所有的整數\(p, q > 1\)},找兩個整數相乘在一起的稱作合成數
\(12653 = 123 \times 111\),可以看到如果有給\(p,q\)這兩個通常稱作certificate(證據)的話就可以在多項式時間內驗證合成數
但要注意也並不是每個問題都能夠在多項式時間裡驗證
定義:存在一個演算法針對language A的驗證者(verifier) V,其中\(A = \{ \omega | V\) 接受 \(<\omega, c>\)針對某些字串\(c\}\)
- 一個多項式時間的verifier執行驗證長度\(\omega\)的字串在多項式時間內
- 一個language A是多項式可驗證的話代表這是一個多項式時間的verifier
- 一個verifier使用額外的資訊\(c\)來驗證字串\(\omega\)屬於A的集合成員
- C: 證據(certificate)或者可以用來證明屬於A的集合成員
定義:NP是一個擁有多項式時間驗證者的language集合,代表可以在多項式時間內驗證完,但不保證能夠在多項式時間內找出答案
NP: Non-deterministic Polynomial time
定義:\(NTIME(t(n)) = \{L|L\)是一個language可以被Non-Deterministic TM在\(O(t(n))\)時間內被決定(decided)\(\}\)
定理:一個language如果在NP裡面的話若且唯若會被Non-deterministic polynomial time Turing Machine被決定(decided)
證明:
\((\Rightarrow)\):使\(A \in NP\)以及證明A會被NTM N所決定(decided).
根據NP的定義讓V是一個多項式時間驗證者針對A
首先假設V可以對輸入長度n的執行驗證時間在\(n^{k}\)的時間內
開始來建構這個N:
N = 可以輸入長度n的字串\(\omega\)
- Non-deterministically去猜長度\(n^{k}\)的字串c
- V執行驗證猜的這個字串\(<\omega, c>\)
- 如果V可以接受,輸出ACCEPT,反之亦然,輸出REJECT
\((\Leftarrow)\):假設A可以被NTM N在多項式時間內所決定(decided)並且建構出多項式時間驗證者V功能如下:
- 模擬N輸入\(\omega\),處理c的每一個符號像是Non-deterministic的方法一樣
- 如果Non-deterministic的branch可以accept,輸出ACCEPT,反之輸出REJECT
推論:\[ NP = \bigcup_{k}NTIME(n^{k}) \]
NP問題範例
定義:clique是一個無向圖,而這個圖內每兩個點(node)必定存在一條邊(edge)
- 一個k-clique代表clique裡面包含k個點(nodes)
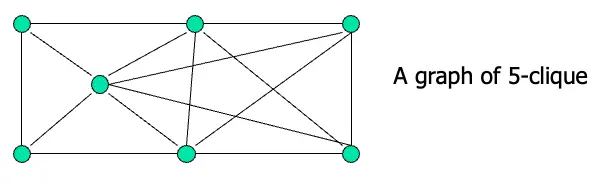
定義:CLIQUE = {<\(G, k\)>|\(G\)是一個無向圖擁有k-clique}
- 定義:CLIQUE屬於NP
證明:
N = 輸入\(<G, k>, G\)是一個圖:
- Nondeterministically猜一組\(G\)裡有\(k\)個nodes的子集合\(c\)
- 測試\(G\)是否包含所有的邊都連接這條\(c\)
- 如果包含的話輸出ACCEPT,反之輸出REJECT
定義:SUBSET-SUM = {\(<S, t>|S = \{x_{1},…,x_{k}\}\)以及對於某些\(\{y_{1},….,y_{k}\}\subseteq S,\sum y_{i}=t\)}
例如:<{4, 11, 16, 21, 27}, 25} \(\in\) SUBSET-SUM, \(\because 4+21 = 25\),可以注意到\(S\)跟\(\{y_{1},…..,y_{k}\}\)可以是多組子集合 定義:SUBSET-SUM \(\in\) NP 證明:N = 輸入\(<S, t>\)
- Non-deterministically猜一個S裡面的子集合c
- 測試\(c\)是否是一個可以加總出\(t\)的集合
- 如果以上兩點都成功就輸出ACCEPT,反之輸出REJECT
所以我們稍微做個小結
P = 問題能夠被快速(polynomial)決定(decided)出來結果的language類別
NP = 問題能被快速(polynomial)驗證(verified)出來結果的language類別
而電腦科學從1950年開始發展至今一直都還沒有嚴謹證明出來的Open Problem
\[ P \overset{\mathrm{?}}{=} NP \]
P到底等不等於NP?