Table of Contents

• Scenario for Security
• Intuition
• Definition

When Ralph C. Merkle proposed “Secure Communications Over Insecure Channels” in 1978 (https://dl.acm.org/doi/10.1145/359460.359473), we began to consider the existence of adversaries eavesdropping on our communication channels over the internet, and we started thinking about how to obscure our data

Scenario for Security

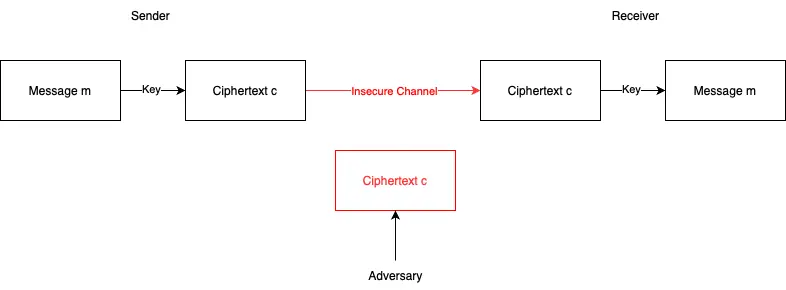
In a traditional communication channel, there are three main components: the sender, the receiver, and the adversary. The sender uses a shared key to encrypt the message  and sends the ciphertext  to the receiver through an insecure channel.

For simplicity, we are not considering the process of key negotiation; instead, we assume that the receiver already possesses the shared key and can decrypt the ciphertext  to recover the original message .

While the ciphertext  is transmitted over the internet, an adversary  exists who can eavesdrop on the channel, observe the ciphertext, and intercept a copy of it for their device.

Intuition

A scheme  achieves perfect secrecy if observing the ciphertext  has no effect on ‘s knowledge of the message  that was sent. This means that  is useless for obtaining  and reveals nothing about 

Definition

An encryption scheme with message space is perfectly secret if for every probability distribution over , every message and every ciphertext for :

If the ciphertext  is useful, it would hold that 

This is because an adversary could obtain some ciphertexts and is assumed to already know the distribution of the message space , denoted as .

The adversary then tries to guess a specific message  from the message space . However, if having access to the ciphertext space  provides no additional advantage for the adversary in guessing this specific message, then the distribution  would be equivalent to .

This implies that the message space  and the ciphertext space  are independent. This concept is known as Perfect Secrecy.