目錄
前言
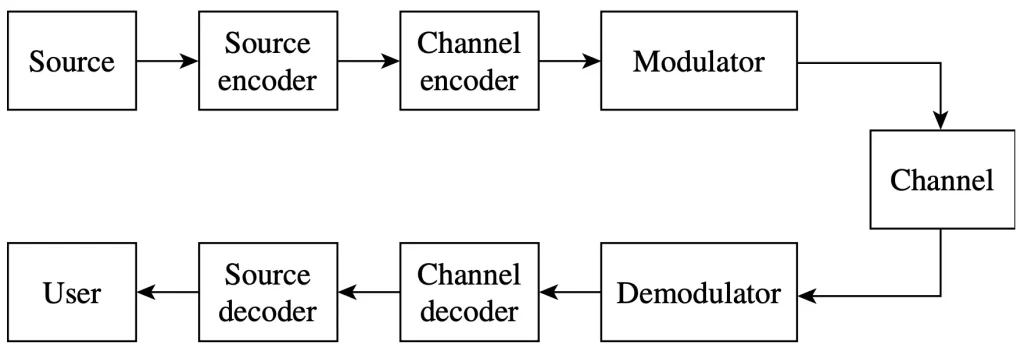
在密碼理論研究當中有兩個特性對於安全的密碼系統來說是不可或缺的,分別是混淆(confusion)以及擴散(diffusion)這兩種特性,由Claude Shannon提出利用這兩種特性是想要抵抗密碼分析上被統計出明文的情況,confusion應用在對稱式密碼系統當中想要讓明文以及輸出密文之間的局部關聯性隱藏起來,其實就是用密鑰來對要加密的資料做影響,而diffusion則是要防止攻擊者能夠利用密文的統計性質找出對應的明文。
儘管在早期有些工程師覺得只需要做confusion-only或者diffusion-only的密碼系統,但Shannon還是認為兩個特性並存的對稱式密碼系統才稱得上足夠安全且加密出有意義的嚴謹密文,在當時1945年的計算機效能下Shannon透過消息理論的技巧就已經計算出密文的資訊量其實會洩漏明文的意義,便提出這種先見之明,畢竟時至今日密碼分析技巧其實每年都在提升,而只包含其中一種的區塊式(block)密碼系統是無法進入NIST的標準協定當中的,而另一項重要的理由是這兩種特性其實也會影響到設計cryptographic hash function跟pseudorandom number generator,這些密碼工具的結果必須消除明文密文對之間的關聯性來防止碰撞問題。
混淆 Confusion
混淆想要讓每一個bits跟密鑰做加密運算後得出的密文其關聯性隱藏起來,從而讓任何攻擊者非常困難透過密文去推算出金鑰,以及遵從雪崩效應只要金鑰內其中一個bit改變就會讓密文或大部分的密文結果變換,這項特性的本質是增加密文的模糊性,並且時常用在區塊式或串流式(stream)種類的對稱式密碼系統上。
擴散 Diffusion
擴散想要讓我們改變明文的每一個bit時至少一半以上的密文也會跟著改變,反之亦然,改變密文的其中一個bit至少一半以上的明文也會與原先的不同,遵從著雪崩效應所製造出來這種密碼系統就有著擴散的特性,這是為了達到隱藏明文與密文對之間的統計特性,代表在這種特性的加密函式必須要能夠把明文中多餘或重複過多次的資料消除或壓縮讓密文中看不出某些特定的格式,在區塊式密碼系統當中就需要把明文的結構放進行跟列之間做擴散的處理。
密碼理論角度
所以當Shannon提出這兩種特性時,他覺得confusion必須讓密文跟對稱式金鑰之間的關聯性設計的越複雜越好,而diffusion則應該要消除明文的統計結構與密文之間的對應,要達成以上兩點的話就需要倚賴定義完整且可重複使用的置換(substitutions)以及排列(permutation)工具。
置換要讓某部分資訊(密碼系統裡就是指bits)替換成其他的資訊,而排列就得透過演算法的設計來操控bits的順序,其中要特別注意的是如果拿到的是非均勻分布的明文字串,例如0與1的數量不平衡就必須重新分配字串進更大的結構,才能隱藏密文中所對應的非均勻特性明文字串內容。
而在某些特別嚴謹的密碼系統上,任何隨機輸入的字串如果其中第\(i\)個位置的bit翻轉(\(0 \rightarrow 1, 1 \rightarrow 0\))的話,其他第\(j\)個位置的輸出bit至少有50%的機率會改變,這種被稱作嚴謹雪崩標準(strict avalanche criterion),這代表著一組固定集合的字串bits會存在50%的機率能夠改變每一個輸出bit字串。
所以理論上來看confusion過的效果會讓攻擊者即便拿到非常大量透過同一把對稱式金鑰加密出來的明文密文對資訊,在多項式時間內也找不出來金鑰的內容,所以在對稱式密碼系統上密文與整把金鑰的關聯性應該會非常高,透過整把金鑰對不同的bits以及利用不同的方法來做加密,一個有效率且足夠安全的加密演算法要能夠在只改變金鑰其中一個bit之後整個密文字串完全改變才稱得上合理的密碼系統。
對於基礎密碼研究推薦Dan Boneh在史丹佛大學開設的密碼學課程:https://www.coursera.org/learn/crypto