目錄
- 數位資料傳輸
- Source and User(or Sink)
- Source encoder and source decoder
- Channel encoder and channel decoder
- Modulator and demodulator
- Channel
- 觀察
- Reference
數位資料傳輸
我們每天一早醒來的生活中充斥著各種數位通訊系統,最常見的就是手機、透過衛星或光纖傳輸的數位電視、數位廣播、Wi-Fi無線網路、WiMax以及光纖數據機轉送無線網路設備等等
另一個傳送數位資訊的方法讀者應該也不陌生,就是儲存設備,其中包括硬碟、磁帶、CD、DVD、藍光光碟以及快取硬碟,想像對於儲存設備來說要進行通訊的話,就是在某個時間點儲存當下狀態的資料,而到下一個時間點在進行資料的寄送或復原等功能
這兩種方法來看根據使用的情境不同,就有不一樣的實作方法,但最基礎的框架離不開C. E. Shannon在1948年他自己的seminal work提出的”A Mathematical Theory of Communication”[1](他只花一學期的課程時間就想出了影響後世70幾年的通訊領域,屌啊)
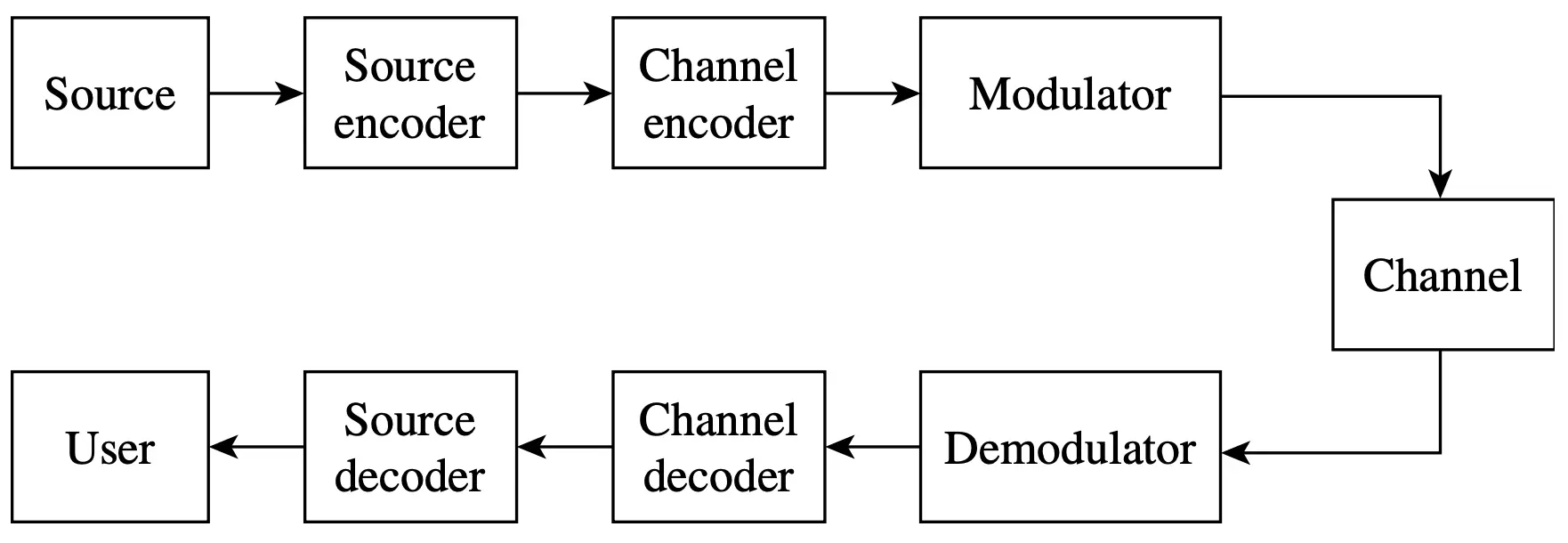
其中最主要的貢獻之一就是提出下面這張圖,用不同的區塊表示基礎的數位通訊或儲存系統應該要具備的能力
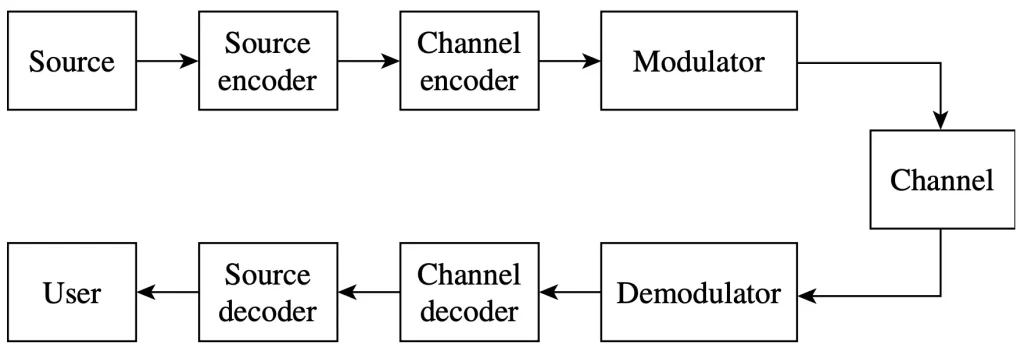
Source and User(or Sink)
想像平時在網路上傳輸的資訊,其原生幾乎都是類比型態的,例如用電話講話時,或者錄下來的聲音,而我們想要在傳送出去的話就必須將這些資訊轉化為數位型態
或者有些本來就是數位波形型態的,例如電腦上的檔案,而要進到通訊通道中,我們一般都預期資料會被轉成一系列的位元型態,接著根據機率模型進行傳送,資料的傳送端有可能是一個人、一部電腦或者某種電子設備
Source encoder and source decoder
encoder會將來源的位元資訊轉成更容易表示的資訊,大部分都是轉成二進位的型態010011001111之類的,好處除了在數位電路中能夠容易處理,同時也可以用更少的位元來呈現,這種做法常常稱作”壓縮”
根據資訊的樣態,如果是電腦檔案的話壓縮時有辦法做到無損,或者影片、圖片或音樂會稍微失真,但最佳的效果能做到難以察覺或可接受的程度,而decoder顧名思義就是跟encoder做相反的事,將原本無損或失真的資訊復原成最一開始的資訊型態
Channel encoder and channel decoder
channel encoder的角色是為了保護位元在傳輸時不受雜訊、失真或干擾所影響,為了達成該目的它會將原先的輸入位元資訊再多加上一些冗位元,提供免疫機制來對抗各式各樣的損害
進到encoder裡面的位元跟被捨棄掉的位元之間的比例稱作code rate,又或者用\(R\)來表示,其中\(0<R<1\),舉例來說一組code裡面其中1000-bits的codeword只有500-bits是information word,則\(R = \frac{1}{2}\),剩下的500-bits就是冗位元
反之,channel decoder要復原輸出位元成原始資訊經過encoder之前的狀態,即使經過傳輸後存在雜訊、失真或干擾的影響也要還原成只有壓縮的位元
Modulator and demodulator
modulator把channel encoder過的位元資訊再轉成適合通道傳輸的格式,舉例來說,對於無線通訊通道,把原始的位元資訊調變成高頻訊號,對於天線來說才更方便傳輸大量的波形
另一種需要調變的例子是資料儲存,某些資訊經過modulation encoder輸出可能受限於連續長度,例如連續相同字元的限制,或者特定頻譜上的限制,例如在DC中出現null,而demodulator的工作就是復原成調變之前的資訊內容
Channel
在modulator調變完之後傳輸的物理媒介就是通道了,或者有時用來儲存資訊,在通訊領域中長期的經驗觀察到傳輸通道經常出現雜訊又時常會被其他通道的訊號干擾,儘管有時影響的程度較輕微,但失真卻是不可避免的
數位通訊的最終目的是為了將通道變成機率設備,從而觀察我們在傳輸過程中的效率,以物理上來看,我們可以選擇的媒介有天線、放大器以及過濾器,要求傳送方跟接收方都要用一樣的系統才能運作,而對於硬體裝置來看,這個通道就必須包含讀寫頭、電磁媒介、讀取放大器以及過濾器等等
觀察
我們觀察到Shannon提出的這個model,其實並不包含近代需要的加解密、時序訊號復原以及信號變更等等區塊,對於目前的設計上來說加解密算是非必要的,而另外兩個則是現代機率傳輸模型在理想上應該要具備的
但作為開山始祖Shannon提出這個概念時至今日還是很受用,尤其將整個機率模型用數學就可以表達的貢獻更是無法忽視,我們將這整個機率傳輸模型稱作參數\(C\),又或者稱作channel capacity,用來測量經過該通道後有多少資訊被成功傳輸,我們可以想像成水管傳輸水量的能力
雖然通道模型\(C\)可以用數種方法來測量單位,但我們目前的情境就限縮在測量code rate \(R\),其單位為每通道位元中的資訊位元
Shannon在他的研究[1]中證明了滿足code rate \(R < C\)則存在一組隨意輸入的可信賴通道,就像傳輸的水量比水管的管徑還小所以任何時間點都能夠成功輸出,另外Shannon也證明反方向,如果\(R > C\)的話則不存在任何Codes可以進行可信賴的通訊傳輸
Reference
[1] C. E. Shannon, “A mathematical theory of communication,” in The Bell System Technical Journal, vol. 27, no. 3, pp. 379-423, July 1948, doi: 10.1002/j.1538-7305.1948.tb01338.x.