內容目錄
當我們在進行異常檢測時,通常會需要注意三個條件:
- 正確的偵測:檢測到的異常資料需要與流程設計想要找到的異常資料是一致的
- False Positives:檢測過程都是正常的,但將一些系統原先就會出現的noise當成異常
- False Negatives:過程中其實有檢測出異常資料,但並沒有紀錄,因為跟noise相比之下實在太過於薄弱,難以辨別究竟是noise還是outlier
Confusion Matrix
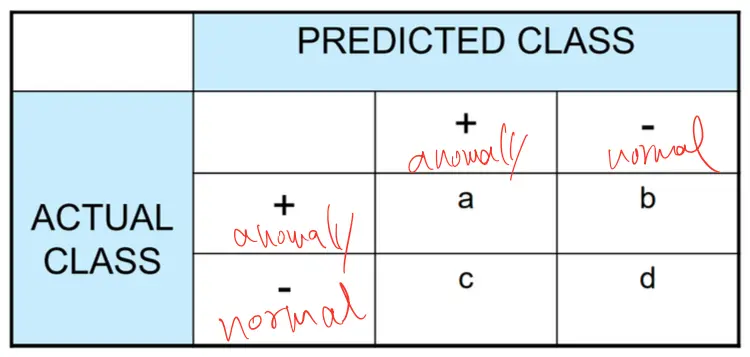
因為我們探討的是異常檢測的問題,所以\(+\)表示為異常值,\(–\)表示為正常值,並且表中還有一些符號是
- a: TP(True Positive)
- b: FN(False Negative)
- c: FP(False Positive)
- d: TN(True Negative)
以及傳統常見的分類方法計算出來:
\[Accuracy = \frac{a+d}{a+b+c+d} = \frac{TP+TN}{TP+TN+FP+FN}\]
這類計算方法使用在許多的問題上,然而在異常檢測的問題上光用這套方法會忽略掉一些東西,試想一些異常檢測在進行準確度的限制,假設negative資料的數量是9990,而positive資料的數量是10,如果model想要預測的是normal class,最後預測的結果出來是\(\frac{9990}{10000} = 99.9\%\), 而你可以注意到這樣的結果其實已經誤導了因為根本忽略掉那些真正的異常值,以及其他常見的評估方法例如像是
- Precision (P) = \[\frac{a}{a+c}\]
- Recall (R) = \[\frac{a}{a+b}\]
- F-measure (F) = \[\frac{2rp}{r+p} = \frac{2a}{2a+b+c}\]
- Weighted Accuracy = \[\frac{w_{1}a+w_{4}d}{w_{1}a+w_{2}b+w_{3}c+w_{4}d}\]
如果只使用以上傳統的評估方法似乎會讓真正的異常值埋沒在資訊當中,所以之後有提出另一種方法
RankPower Metric
\(R_{i}\)表示成在整個排序好的rank list當中第\(i\)個最可疑的異常值,在這個rank list當中越靠近前面的值要是最有特徵的異常值,使得RankPower計算成
\[RP = \frac{m_{t}(m_{t}+1)}{2\sum_{i=1}^{m_{t}}R_{i}}\]
其中\(m_{t}\)就是決定異常值最大範圍取多少出來,rank list在排序過後,希望是\(1, 2, 3,…, ,m_{t}\)這些越靠前面的值越像異常值,而越靠後面的代表越像正常的資料,而在取樣\(R_{1}\)到\(R_{m}\)代表著取出來\(1, 2, 3,…., m_{t},….\)取出最多到\(m_{t}\)個資料就像
\[\Rightarrow \frac{m_{t}(m_{t}+1)}{2}\]
而因為會跟所有取樣的做相比,所以會map到\([0,…,1]\),最佳的結果是取\(m_{t}\)個位置的資料全部都是真正的異常值時可以算出來是1,RankPower如果取樣精確的話精準度會比前面幾種方法都還要來得好。
但我們舉個例子,假設dataset \(\mathcal{D}\)擁有的size \(n = 50\),其中裡面存在\(5\)組真正的異常值。
假設一組anomaly detection演算法偵測出\(m=10\)組資料點是異常的,而\(m_{t} = 4\)才是真正異常值,在這個條件下,讓\(\mathcal{D}\)裡真正的異常值出現的rank位置是\(\{1, 4, 5, 8\}\),我們計算一下
\[Pr = \frac{4}{10} = 0.4, Re = \frac{4}{5} = 0.8 \> and \> RP = \frac{4 \times 5}{2(1+4+5+8)} = 0.56\]
可以看到用RankPower並不是最佳的選擇,因為在這個問題之下我們忽略掉了其中一組異常值,使得RankPower的精確度無法達到最佳,但有時候也還是會採用,根據你的問題可以決定要不要承擔捨棄掉一些難以辨別的異常值。
另外在介紹一種curve是許多研究人員都會使用的方法,叫做
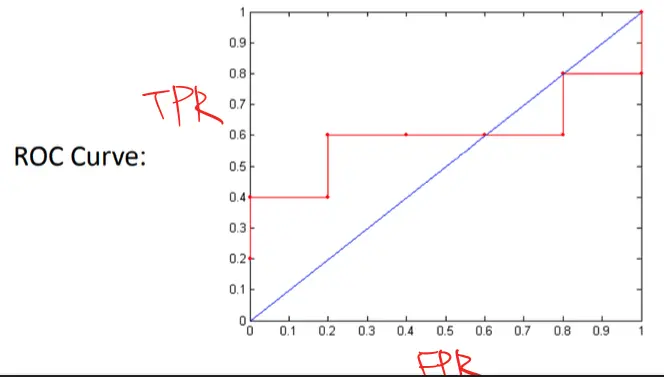
Receiver Operating Characteristic (ROC) Curve
透過True Positive Rate(表示為y軸)以及False Positive Rate(表示為x軸)互相繪製出來的曲線,其目的在於顯示當threshold的參數調整時,繪製分類出來的問題其效能曲線圖,透過TPR以及FPR作為點。
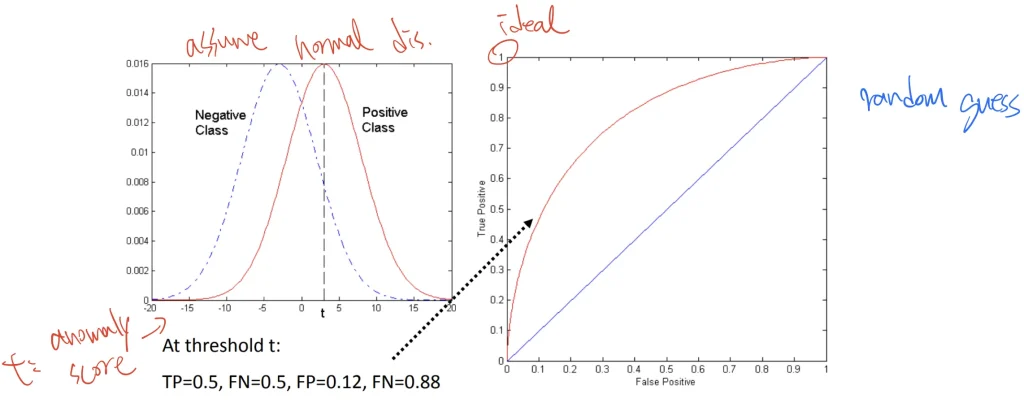
上圖使用的資料是相同的,但改變了threshold的演算法以及使用了不同的取樣分佈所以讓點的位置不同
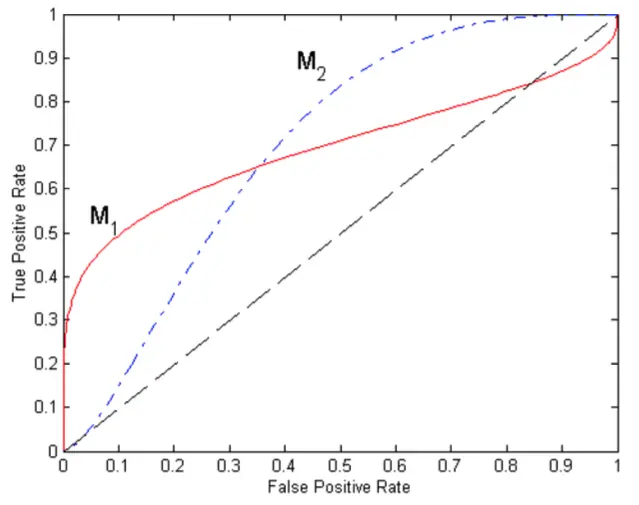
但至於要使用哪一種分佈,由上述的圖片顯示比較兩種不同的方法,可以看到\(M_{1}\)在較低的FPR中表現較好,而\(M_{2}\)在較大的FPR表現較好,面積下最理想是到達\(1\),而隨機預測的面積是在\(0.5\)。
而該如何建構一個ROC Curve?
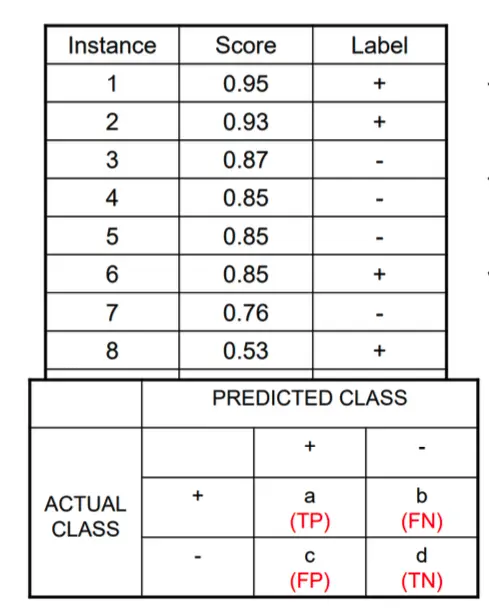
首先會先決定好一些initial的instances,而用這些參數來計算異常值,排序好這些初始值後,再來決定每一組值的獨立threshold
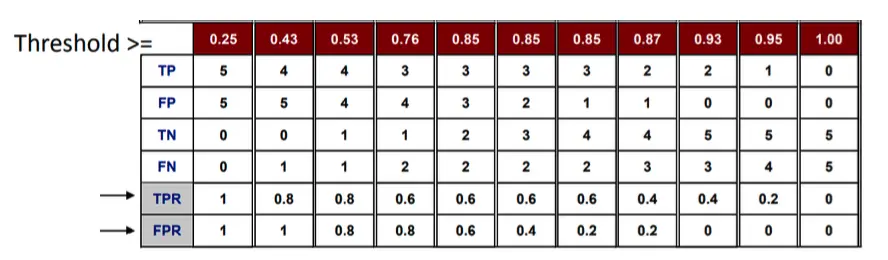
最終我們可以計算不同threshold之下的TP, FP, TN, FN
\[TP \> rate, TPR = \frac{TP}{TP+FN}\]
\[FP \> rate, FPR = \frac{FP}{FP+TN}\]