目錄

為什麼我們需要亂數？

在密碼理論的研究領域當中，我們非常注重random number的來源，計算過程以及運算完成後的亂度性質，不管從數學性(mathematical)、隨機性(stochastic)、以及量子性(quantum)，另外蒙地卡羅系列的計算、數值分析、統計研究、隨機演算法以及樂透機率等等也都非常倚賴亂數。

像是你我現今生活當中有許多的應用都需要加入亂度，諸如手機通訊裡的演算法、電子郵件加解密的存取、網路電子支付通訊加密等等，乃至於一般網路安全通訊以及分散式電網安全系統(SCADA)都需要。

亂數產生器

科學家們早在很久之前就一直在關注著亂數產生器(Random Number Generators)，在數學研究領域上確實也存在一個分支是在探討何謂亂數？以及如何取得這些亂數？

在數學上有方法可以證明，但在John Von Neumann所發明的von Neumann架構上圖靈機必定是deterministic的，這在演算法的書上意味著我們目前在現實世界中所有使用的計算機都無法產出真正的亂數

Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin.

時至今日，亂數產生器還是一個受到蠻多關注的研究題目，主要的問題是我們還是缺少嚴謹的證明亂數夠亂，以及還沒找到能夠不斷重新製造你證明為亂數的方法。

而主要有兩種方法可以製造亂數：

  • Algorithmic (pseudorandom)
  • Physical
    • Noise
    • Choas
    • FRO
    • Quantum

找上述的兩種方法來看，我們目前其實擁有兩種產生器，第一種為偽亂數產生器 Pseudorandom Number Generator (PRNG)，第二種為真亂數產生器(TRNG)。

偽亂數產生器(PRNG)

偽亂數產生器無法造出超過原先制定的數學公式束縛，並且產生的這些亂數都會是determinisitc的且有週期性順序的亂數，而能造出多少組亂數序列取決於一開始所使用的初始亂度種子(seed)。

真亂數產生器(TRNG)

真亂數產生器通常由物理行為來決定，可能會使用自然界或者硬體上的隨機情形來當作亂度的表現，不同於偽亂數產生器，透過自然界中的現象或者硬體產出的隨機性能夠透過non-deterministic的方法取得資訊，用來當作種子產生亂數不失為一個好方法，而硬體我們可能是從計算機上的不同區域取得後再合併起來，就能夠讓資料數量級變多。

例如像是使用Johnson’s noise, Zener noise, radioactive decay, 二項分光鏡的photon path splitting以及光子穿射時間等等，而簡單評估這些方法取得的不均勻機率的零與一用bias \textcolor{b} 來表示

    \[ b = \frac{p(1) - p(0)}{2} \]

零跟一的機率必須要分散掉，所以bias最好的機率就會是0.5，另外如果取得多種有關聯性的資料，可以進行序列化的自係數調整 a_{k}

    \[ a_{k} = \frac{\sum_{i=1}^{N-k}(b_{i} - \bar{b})(b_{i+k} - \bar{b})}{\sum_{i=1}^{N-k}(b_{i} - \bar{b})^{2}}\]

其中\{b_{1},b_{2},\cdots,b_{n}\}是N個bits長度的隨機字串，而k則為係數的order，每一個bit都與自己的反向係數相減再做normalize把多個係數項機率分散掉

不管是透過b或者a_{k}都是想要讓真亂數產生器產生出來的字串裡的bit關聯性降到最小，從而使得每一次產生的字串都是最理想的亂數，而目前也有一些製造真亂數產生器的研究持續進行當中，粗略的可以找到四種方法：

  • Noise-based RNG
  • Free-running oscillator RNG
  • Chaos RNG
  • Quantum RNG

Noise-based Random Number Generator

此種RNG是由硬體上的元件來製造雜訊例如像是Johnson’s noise就是利用Johnson’s effect在電阻材料終端上當溫度高過零度時會隨機產生的電壓，其中就是利用電荷載子當一定數量的電荷游離到材料另一端的金屬板就能夠產生出隨機的熱能運動。

然而長距離的載子移動其實會由材料導體來決定多少電荷時會進行移動，因為電路在設計上都會考量這些元件的熱能與移動時間，所以材料商其實都會特別設計一定的threshold並且在規格書上標示，所以某種程度上其實完全倚賴電壓並不完全屬於隨機的。

另一種比較常見的是Zener noise或者是稽納二極體，其中主要產生的是Zener effect其在稽納二極體上利用二極體通道區間內的穿遂效應，如果電流足夠低的話，就會在二極體上讓電流穿遂進行電荷的”jumps”動作，以此造出1/f完美隨機的粉紅雜訊。

而反之如果反向電流足夠高的話便會讓二極體出現高的內部潰倍增益，讓電荷快速地回到充電前的狀態，然而由於Zener effect的效果其實還未發現能夠把雜訊跟硬體裝置區給分開來，不管是利用哪種效應亦或是使用量子穿遂方法，問題出在memory effect這個效應會讓從硬體當中抽取出來的亂數之間具有關聯性，材料在使用一段時間後裡面的載體會適應平時電荷的移動速率，從而固定在某段區間內，遲早會造成倚賴這種方法造出的亂數會總是落在某段電荷移動速率區間內。

其他一些方法還有雙極性電晶體的反向發射截斷、雷射相位雜訊以及混亂雜訊等等，然而這些利用材料元件所製造的雜訊都還是有一些問題沒有解決，像是雜訊來源的隨機性無法明確的識別出特徵、被測量或者在元件製造時有效的控制，這在研究上使得我們只能單方面的相信這些亂數是真的雜亂訊號，而不會有某一週期的頻率出現在元件的作動上。

有些雜訊機制是想要先造出極小的電壓後再進行放大，這麼做的好處在於能夠用放大器增強頻寬同時取得nonlinearity的雜訊，進一步的產生有偏差的隨機雜訊，但要小心的是採用電路邏輯上的快速電壓切換來當作訊號，如果存在多個RNG太接近的話可能會發生相互同步作用，導致強烈的電磁干擾讓所有取得的雜訊entropy資訊量降低，而這也給了研究員一個提示，用外部的電磁場就能夠操控高敏感的放大器及其元件從而控制雜訊以及證明亂度。


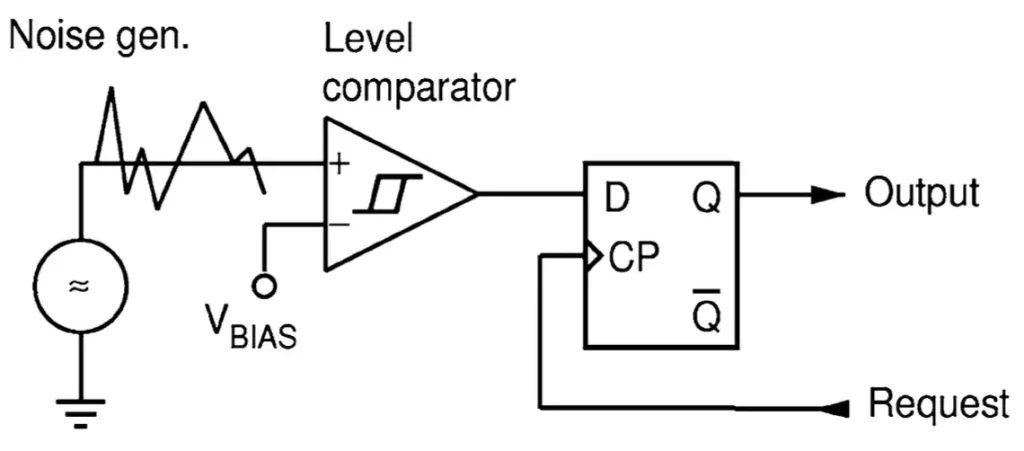
圖一、Noise-basedRNG [1]

即便我們知道可以使用電磁場去控制雜訊的輸出然而要如何微調要控制在哪個threshold還是一件難以克服耗時且無法每次都精確的控制，絕大部分需要靠經驗法則來調整，如果想要造出0.1的bias需要10秒，則想要造出更精確的0.01則需要打十次電磁進去，更甚者想要再更精確的話需要再乘上10倍的時間，而且不是每次控制threshold都能夠如自己預期，所以可能還會需要多重複幾次的動作包含在內。

再者即便我們把精確度壓到0.01之下，可能還是會出現極小的mean值飄移，使得最後拿到的訊號出現不可忽略的bias，這每一種問題都需要靠更精良或者足夠經驗才能一一排除。

如果真的造出來了那還需要考量三種情況：

  • 已開發過後的雜訊來源其亂度的可證明性？
  • 取樣/數位化過程中是否會出現任何效應？
  • Deterministic後處理過後最終可否拿來使用？

許多的研究員針對這三點提出了一些電路，主要是想要提升亂數程度，尤其是bias如下圖


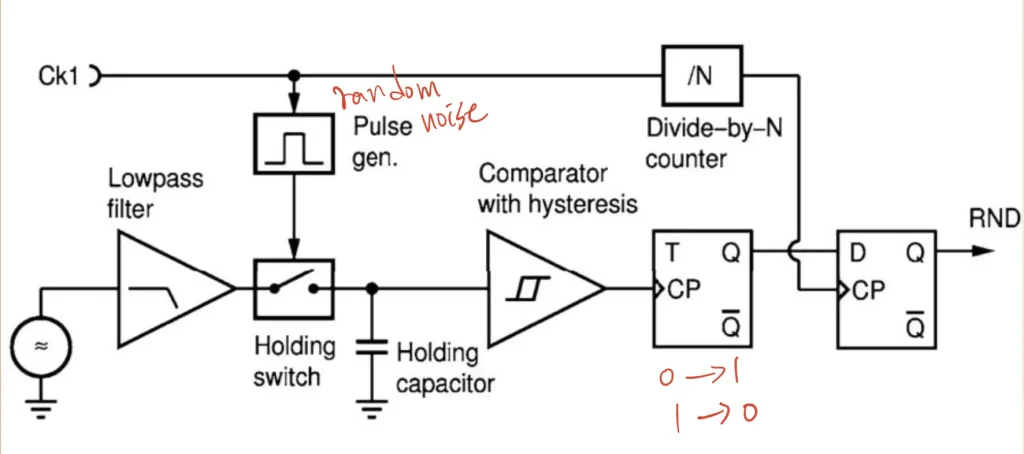
圖二、A zero-bias noise-based RNG [1]

圖二的架構還是存在一些問題，像是電容這種元件其實會記憶前一次類比電壓的狀況，另外如果TFF太常觸發的話，會預期每次都要給一樣的輸出結果，所以通常還需要再加上ck2來讓bit取樣頻率f_{ck2}，其雜訊頻率會比f_{ck1}來得低。


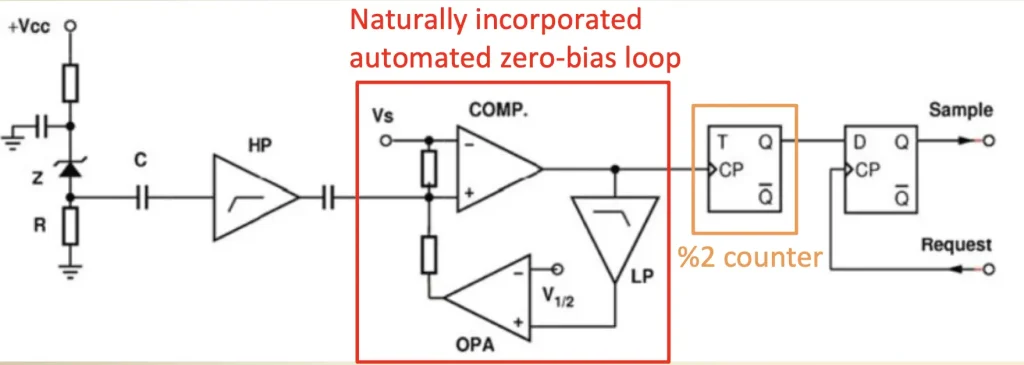
圖三、Another zero-bias noise-based RNG [1]

另一個想法是多加幾個比較器做一個循環來讓隨機信號最後做一個時間加成，而時間會由clk以及元件的傳輸速度來決定，而每一次的速度都會不同如圖三。

以上的雜訊來源都來自電子雜訊，電子元件工程師會嘗試透過這些電子元件以及晶片從而努力去造出更小的雜訊，而對於所有noise-based generators會需要某一些的後處理，如果原始bits出現高強度的關聯性，只靠一些簡單的處理方法是不足消除bits之間的關聯性的，畢竟產生這些亂數字串是依靠bits之間的相互作動所關聯出來的，對於只採用noise的情況來說還是不夠隨機，只要還是持續仰賴物理動作就無法獨立出來，並且還是沒有太過於中立的方法來驗證其隨機性。

Chaos RNG

此種RNG是結合多種deterministic系統交互而成的過程輸出轉為亂數，簡單來說就是依靠混沌理論，透過多種跨領域的科學研究以及屬於其中一種數學分支，專注於潛在的樣式以及動態系統中確定性的法則從而決定高度敏感的初始值，而製造出凌亂並且非常規的完全隨機行為。

圖四、double-rod pendulum at an intermediate energy [2]

所以主要就是想從數個混亂的物理系統重複去測量來取得亂數，造出宏觀程度的雜訊將其當作種子再透過noise RNG的方法產出更多的亂數，而研究上可以使用的物理系統有光學系統、電子系統、光電工程系統等等。

在光學系統裡最常利用雷射所提供的快速混沌系統產生亂數，小型雷射或者共振器以及其他被動主動的光學儀器都能夠完全的整合在晶片當中，雷射所產出的混沌波動輸出功耗可以簡單且快速的達到反射，大約每秒打出300Gb的產生速度，打出去之後用光電二極體進行吸收如圖五

圖五、Choas RNG [1]

如果想要排除電光二極體吸收效率從而讓處理速度變快，也有團隊在研究全光學雷射的RNG，所有的信號以及信號處理都在光學階段完成，將混亂雷射的光子強度當作亂數來源，在光學裝置內所有打出去的信號數位化成亂數如圖六。


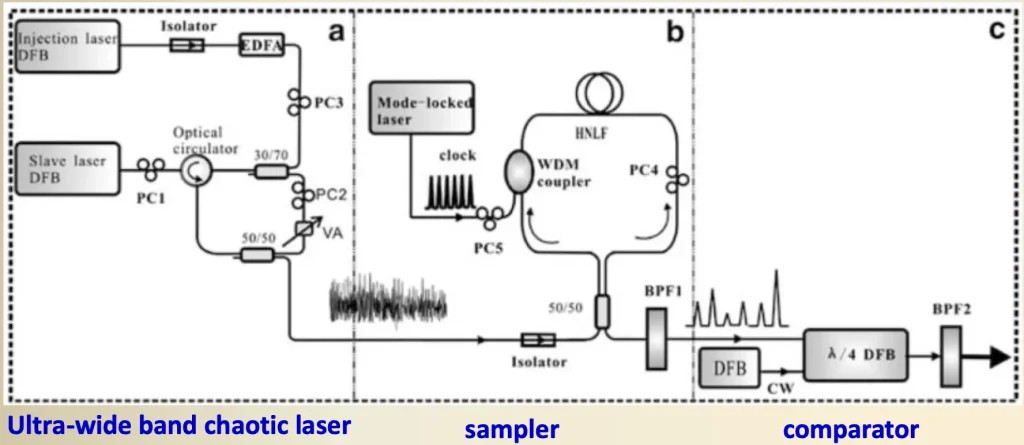
圖六、All-optical laser consisting RNG [1]

圖六是處理一組的雷射信號，而要讓混亂程度上升還可以透過XOR兩種，來讓隨機輸出的bits能夠植基在序列相關上，所要做的就是XOR兩組獨立的RNG輸出bits如圖7

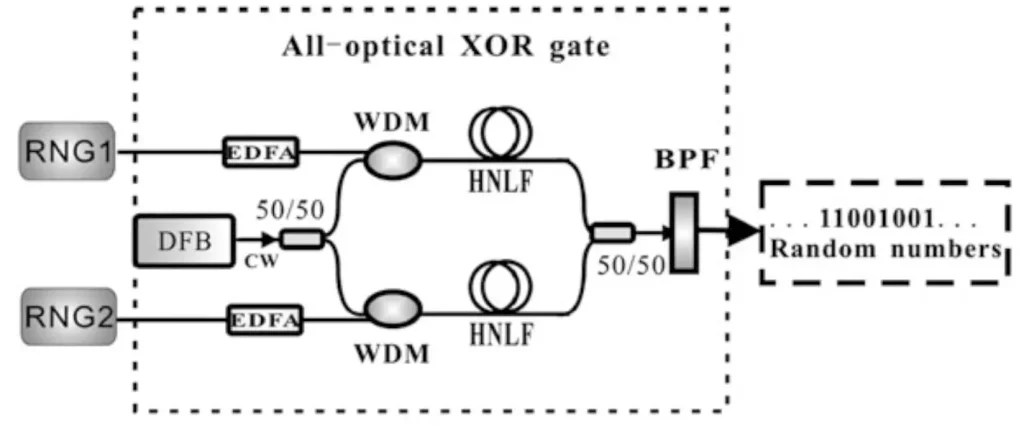
圖七、All-optical XORing of two independent RNG [1]

利用混沌系統的行為是非常特殊的方法，然而透過這種方法所製造的亂數也受限於物理系統的上限，而現有物理系統的公式以及結果所能造出的隨機bits也是有限的。

Free-Running Oscillator RNG

此種RNG是電路上最簡單以及最便宜的方法，主要做法就是將一連串的振盪器串聯在一起，輸出串回成輸入做成一組電子振盪器，通常就稱作free-running osicllator (FRO)如圖八

圖八、Schematic diagram of FRO [1]

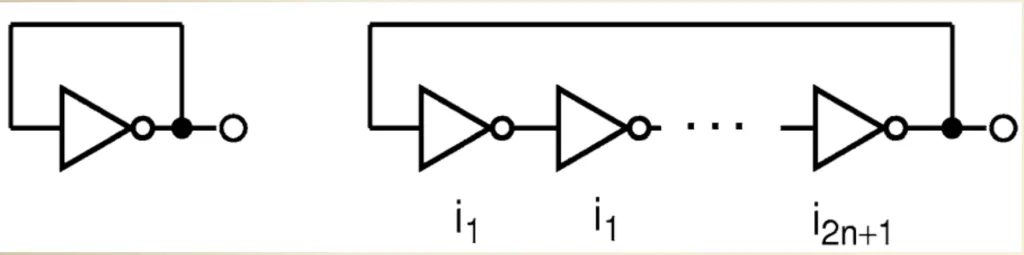
其實我們可以把FRO RNG視為noise-based亂數產生器的一個特例，由於可以接上不同的clk給這些FRO，所以每一個FRO電路其實是獨立運作的，不同的FRO會根據串接的振盪器數量以及元件的差異從而產出不同的頻率，而我們將不同的FRO電路組合起來就會是隨機的結果了，但要注意的是如果每個振盪器太過於接近的話有可能會被電磁干擾導致輸出輸入同步，然而這也是可以拿來利用的特性，可以將反向的輸出信號放大到不可忽略的程度，就能夠將其接收附近的電磁干擾。

利用較慢的FRO取樣來當作較快的FRO輸出，原理在於兩個FRO之間的頻率差距在足夠大之後，會產生出電子抖動，其週期訊號與真實訊號有著一定的差距這誤差值不同的FRO之間會有不同的輸出，而我們將這種輸出當作亂數。

Von Neumann Corrector

通常我們會使用並聯數個FRO經過好幾回合取得隨機字串，而比較簡單可以去除零與一的bias的方法可以使用Von Neumann Corrector，主要做法是一次看兩個bits，輸出條件如下

  • 如果輸入的bits為00/11則不輸出任何東西
  • 如果輸入的bits為01則輸出0
  • 如果輸入的bits為10則輸出1

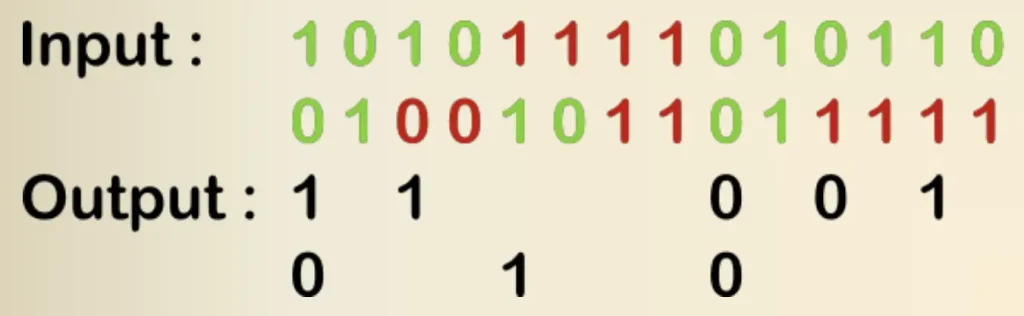
所以以範例來看輸入事1010111101011001001011011111，其輸出照上面的規則來看可以產出11001010，雖然取得的字串變短了但將零跟一的bias給調整到0.5。

而我們提到FRO可以串聯或並聯多組，同時也可以跟其他種類似的電路進行合併，像是跟Linear Feedback Shift Register(LFSR)做結合，就是想讓FRO生成的亂數作為種子，再透過seeded類LFSR PRNG的方法再去產生更多的亂數字串，又或者可以根據不同的結構來做結合，像是Galious Ring Oscillator (GARO)如圖九或者Fibonacci Ring Oscillator (FIRO)等如圖十

圖九、Galois ring oscillator
圖十、Fibonacci ring oscillator

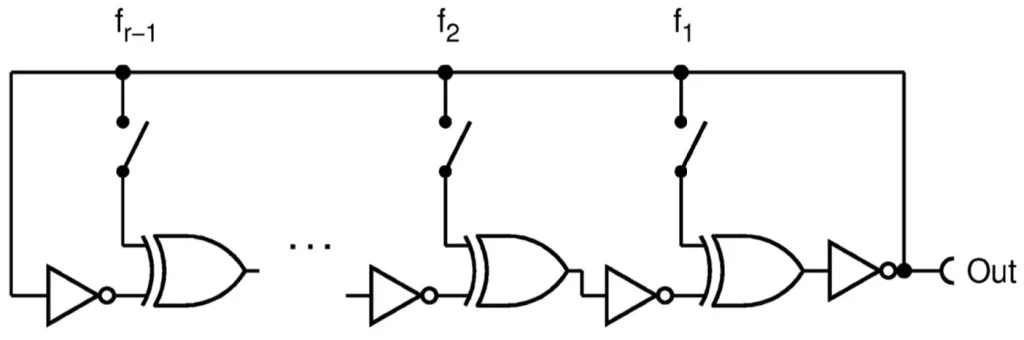
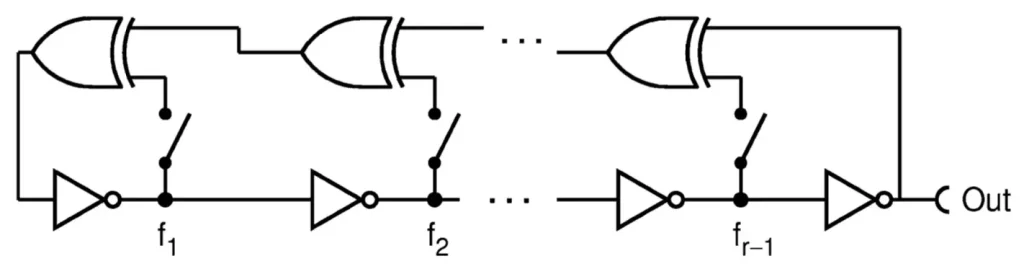
上述兩種很相似的產生器其實可以一併在電路裡實現，並且除了方才提到Von Neumann Corrector可以去除零與一的bias之外，其實透過XOR的動作也可以實現來增強隨機性，只需要將GARO以及FIRO的輸出進行XOR後即可得到比原先兩組各自產生的字串還要更多的隨機性。

然而GARO以及FIRO的問題是需要足夠大的雜訊才能推動電路輸出隨機字串，因為除了原先的相反器之外還新增許多XOR邏輯閘，所以通常在設計上必須要考量整個電路的大小以及時序的分配，尤其對於FRO這種電路環環相扣的設計在晶片的設計上太近會電磁干擾，放太遠又會需要更大的面積，如何製作好的FRO是一門藝術。

Quantum RNG

此種RNG是利用觀測單一隨機量子效應來製造隨機bits，這種方法主要就是想要依靠量子物理的特性，在觀測兩個不同的量子態(quantum state)之前會處在一樣的狀態，然而去測量這兩組量子態之後各自的狀態就會進行改變，在現有量子計算的研究上最常使用的是利用光子所製造QRNG，因為只需要延續之前的光學研究就行，不過這次打進去的是量子態。

圖十一、Spatial principle QRBG

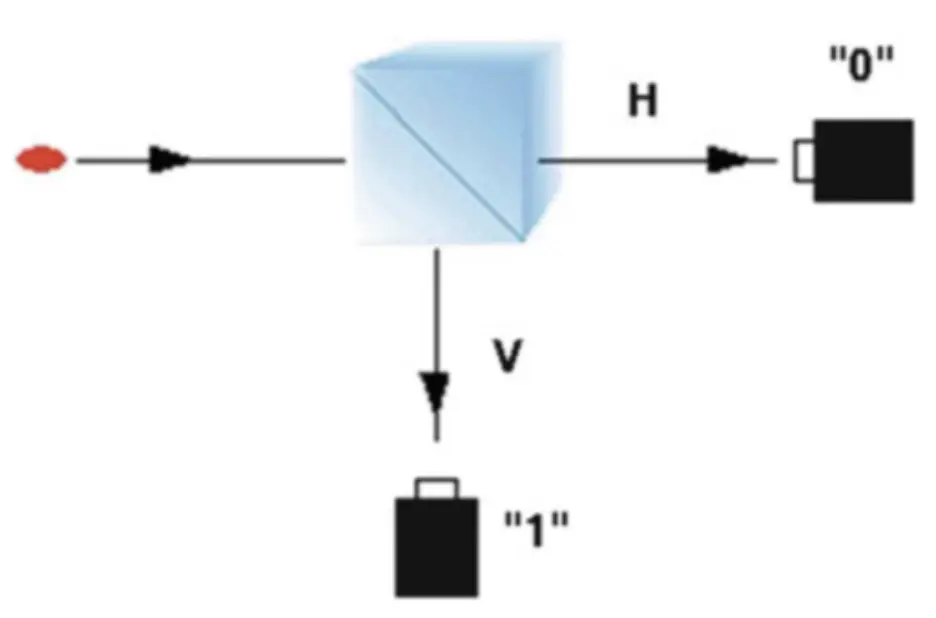
原子束分裂的QRNG是將循環的偏光光子打進偏光原子束分裂器，分解掉入射光的偏振，而目前這種方法的問題是初始的差異以及打進去的光隨著時間以及溫度會漸漸地影響到亂數的bias，所以後來又有人想到用控制溫度的方法如圖十二

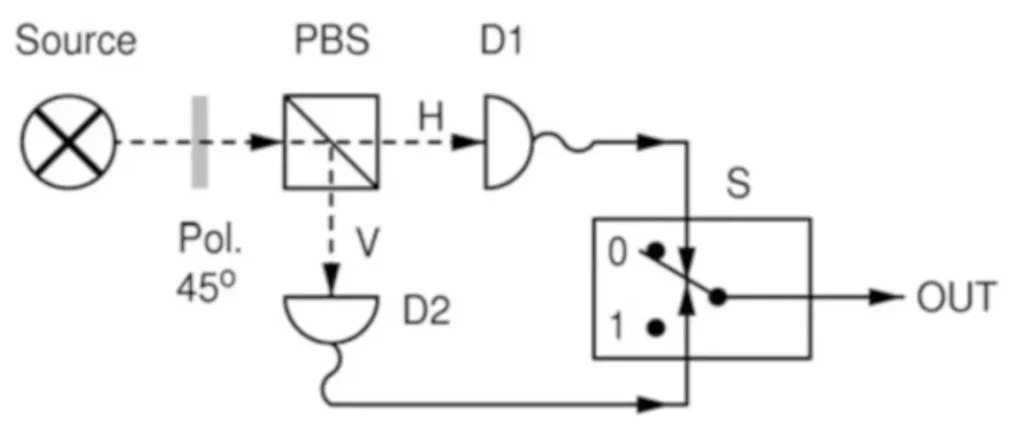
圖十二、Optical quantum random number generator

然而這使得bias更加的不穩定，而且對於溫度的變化更加敏感，受限了可以收集亂數的時間，從而導致了收集而來的不同亂數字串之間的隨機bits有了關聯性，這點跟noise-based RNG的情況一樣。

TRNG後處理

我們在上述提及了四種真亂數產生器的方法，然而我們也在開頭講了目前其實沒有一個很嚴謹的證明方法可以證實說我們從自然界或者硬體材料當中取得的這些亂數字串是否真的為亂數，而從研究員的角度來看也許我們必須先假設這些TRNG永遠無法產出完美的亂數，所以我們通常會需要使用到後處理的方法。

後處理需要設計一定的複雜程度來讓我們收集到的亂數字串能夠消除不完美性，但要記住的是

我們現在所生活在的這個Cryptomania世界當中是無法造出真正的完美亂數

雖說要複雜但也是需要透過計算機來執行後處理的演算法，主要透過犧牲一部分的bits來取得雖然更小但更於隨機的集合

而其中一個好的TRNG通常只會需要post-processing-free或者只需要simple post-processing即可，主要技巧有四種：

  • Ad-Hoc Simple Corrector
  • Cryptographic Hash Function
  • Extractor Algorithms
  • Resilient Function

Ad-Hoc Simple Corrector

corrector如之前有提到的XOR兩組不同的隨機字串或者是相鄰的兩個bits做XOR，這種好處是可以平行的去計算XOR，另外有時候如果零與一bias太高的話也許能夠忽略一些bits，以及上面有提到的von Neumann corrector的方法來去差異化，最後可以透過輸入不完美的亂數字串進去LFSR消除差異性。

然而如果初始字串存在著關聯性，用de-biasing的方法可能還會增加更多的bias或者其他統計上的缺陷進去，例如像是von Neumann de-biasing的方法如果今天輸入的字串是10101010….，不存在任何的bias在裡面的話進行後處理最後會輸出成1111….，就會造成最大的偏誤以及相依性。

Cryptographic Hash Function

又可稱作one-way hash function這個在密碼理論的研究上很常見，屬於一個數學性的function，在輸入一個不限長度的隨機亂數後從這個function裡的域映射(domain)到另一個域(domain)，不過從軟體上實作當然沒問題，然而如果今天要在硬體上實現的話會受限於硬體晶片的資源短缺，而一個好的hash function應該要能夠抵抗統計上的碰撞問題。

Extractor Function

一個隨機性的擷取器可以用一個演算法轉換一組較弱的隨機序列變成一組較短但隨機性較強的字串，會想要使用這種方法最初在於後處理階段時增強TRNG的穩定性，針對元件的老化、溫度的變化以及硬體上的攻擊所導致隨機字串輸出時看起來是足夠的，然而查看bias卻發現有不平衡的狀況，不過擷取器演算法的問題還是需要一些記憶體的空間以及大量的CPU運算資源來進行後處理，使得硬體計算情況變得複雜以及輸出bit的速度變慢。

Resilient Function

Resilient function主要是想要過濾掉任何可能被攻擊者所操控製造出來的deterministic bits，通常表示成(n, m, k)-resilient function，這個function的動作是f: F^{n} \rightarrow F_{m}，當輸入k個bits進去固定而其餘的n-k個bits都為隨機亂數，其中有可能輸出m元組的情況會發生，這個function想要找出來m-tuple的bits，從而偵測出是否有被操控的嫌疑，其中F \in \mathcal{F}_{2}。

Reference

[1] Stipčević, Mario & Koç, Çetin. (2014). True Random Number Generators. 10.1007/978-3-319-10683-0_12.

[2] Wikipedia. Chaos theory. https://en.wikipedia.org/wiki/Chaos_theory#