目錄
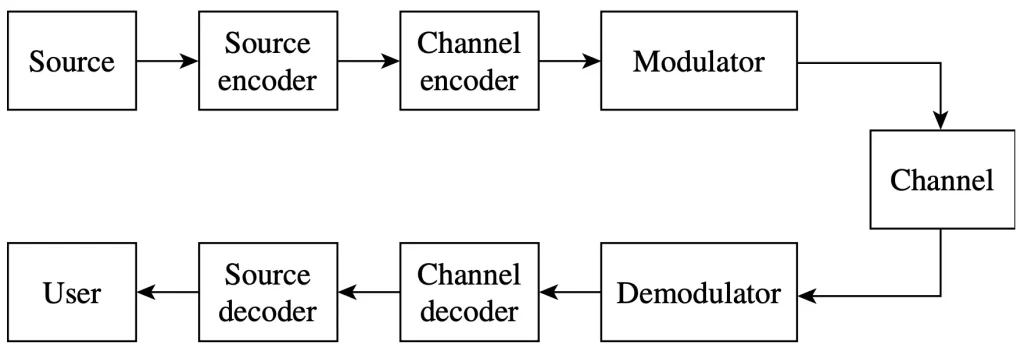
Multi-tape Turing Machine
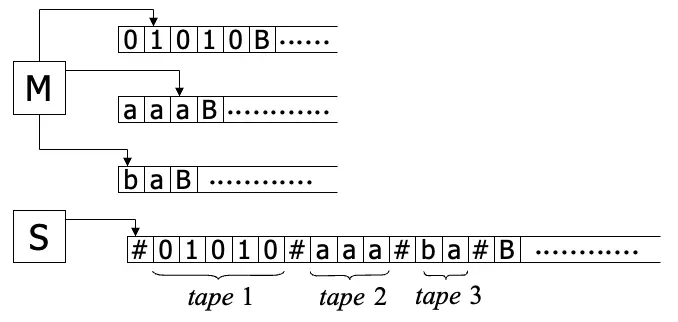
在單一的tape裡面存在多組tape,另外每一個tape都由各自的讀寫頭來進行控制,在規範各個tape之間使用的alphabet即可。
Non-Deterministic Turing Machine
\(\delta: Q \times \Gamma \rightarrow \gamma(Q \times \Gamma \times {L, R})\)
定理:任何non-deterministic Turing Machine等同於Deterministic Turing Machine
證明步驟如下:
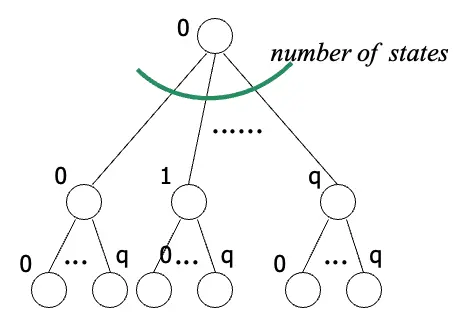
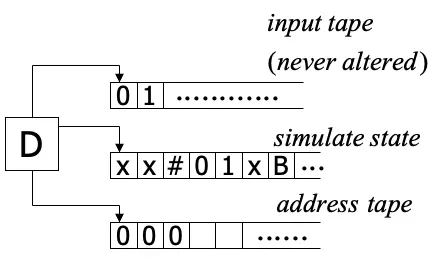
- 初始tape 1包含輸入w的字串,tape 2跟tape 3先塞空字串
- 複製tape 1的內容到tape 2
- 使用tape 2在一條non-deterministic計算之下去模擬w的N個輸入,先查看tape 3下一個symbol的位置之前來決定讀寫頭如何移動,如果已經沒有符號在裡面了就進到步驟4,如果reject也進到步驟4
- 增加tape 3的次數,回到步驟2
推論1:一個language可以被non-deterministic Turing Machine給識別(recognizes)的話若且唯若稱這個language是Turing-recognizable
推論2:一個language可以被non-deterministic Turing Machine給決定(decides)的話若且唯若稱這個language是decidable
Enumerators
讓Turing Machine多一個可以列印的元件,language產生的所有字串都可以被enumerator給枚舉出來
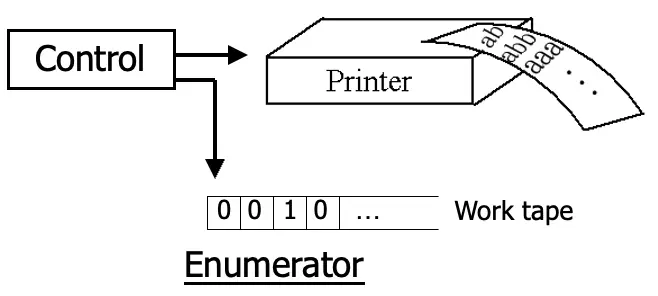
定理:一個language可以被某些enumerator給枚舉language裡所有的字串若且唯若稱這個Turing Machine是Turing-recognizable
證明:
- 如果一個Enumerator E可以枚舉language A同時存在一個TM M可以recognizes這個A,M = 輸入w
- 執行E,比較E產出來的字串跟w是不是相同
- 如果w全部的排列組合都被E給輸出完就代表accept
- 如果Turing Machine M可以recognizes一個language A,同時也可以建構屬於A的enumerator
存在\(S_{1},S_{2},…\)屬於\(\Sigma^{*}\)所有可能的字串,E = 無視所有輸入- 重複i = 1, 2, 3, …
- 根據\(i\)的步驟執行\(M\)產出\(S_{1}, S_{2}, …, S_{i}\)
- 如果任何計算都是accept的話,輸出相關的\(S_{i}\)