消息理論中的熵

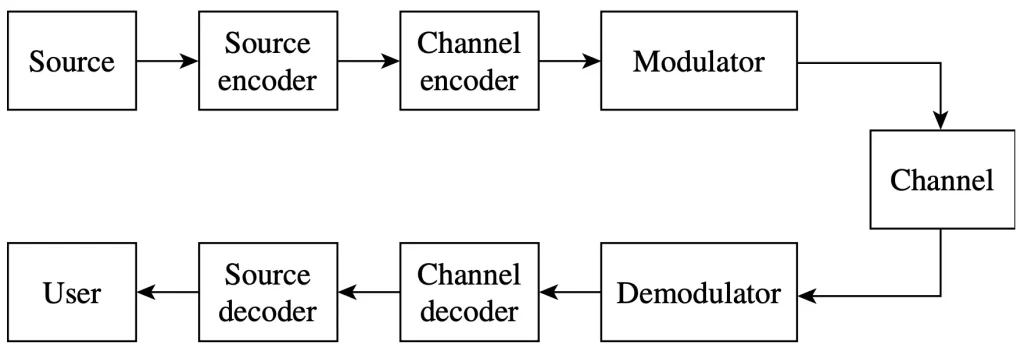
目錄

• 定義
• 範例

我們在消息理論測量一段資訊所包含的資訊量其中一種會使用Entropy來計算。

定義

讓$X$作為一個discrete R.V. 並且表示成$P(X)$可以視作:

$$H_{b}(X) = -\sum_{x \in \mathbb{X}} P(x) \cdot log_{b}P(x) = \mathbb{E}[-log_{b}P(X)] = \mathbb{E}{p} [log_{b}\frac{1}{P(x)}]$$

1. b如果選擇2就表示我們在測量bits，若b是e則表示在測量nats，所以這裡沒有直接寫2是因為可以透過換底公式來換成別的格式。
   換底公式: $log_{b}P(x) = log_{b}a \cdot log_{a}P(x)$，因此，$H_{b}(X) = (log_{b}a) \cdot H_{a}(X)$，不過我們在消息理論內幾乎都是在談b=2的情況。
2. $H(X)$測量的是$X$剩餘的不確定性，把$x$所有的可能性平均起來
3. $H(X)$不是一個隨機變數$X$的function，而是針對PMF隨機變數$X$分佈function進行量測
4. 根據$lim_{x \rightarrow 0} \> xlogx \rightarrow 0$,定義 $0log0 = 0$,因此如果新增了0的機率並不會讓entropy有任何變化

範例

假設$X$有Bernoulli(p)的分佈，i.e., $x = \begin{cases} H, & \mbox{with probability} & \mbox{P} \\ T, & \mbox{with probability} & \mbox{1-P} \end{cases}$ 在投擲硬幣的時候呈現這樣的分佈

$$H(X) = -P \cdot logP – (1-P)log(1-P) \triangleq H(P) \> binary \> entropy$$

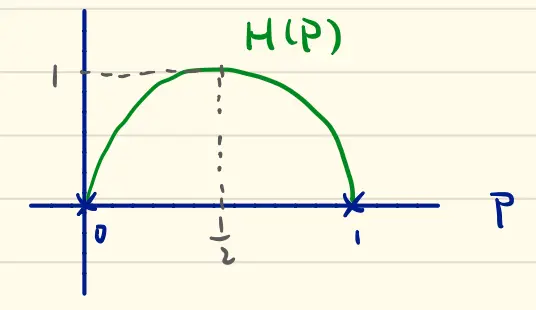
我們觀察這個分佈圖

1. $H(P) \geq 0$ 在P=0或是1的情況時會發生 (在結果變成deterministic的時候發生代表全部的不確定性已經消失)
2. $H(P) \leq 1$ 在$P = \frac{1}{2}$的情況下會發生 (如果是一個公平的擲硬幣0跟1兩者最高機率都會是$\frac{1}{2}$的最大不確定性)
3. $H(P) = H(1-P)$ ($P$要稱為head或是tail都不重要，這裡要表達的是只要結果是0跟1的事件都可以使用這種方法)

另外有一些定理存在

1. (Non-negativeness): $H(X) \geq 0$ 成立若且唯若$X$是一個deterministic
2. (Maximum entropy): 讓$X$是一個discrete隨機變數屬於有限的alphabet $\mathbb{X}$，存在$H(X) \leq log|\mathbb{X}$若且唯若$X$有uniform distribution的特性在$\mathbb{X}$之上

證明：

1. (Non-negativeness): $$0 \leq P(x) \leq 1 \Rightarrow \frac{1}{P(x)} \geq 1 \Rightarrow log\frac{1}{P(x)} \geq 0, \forall x \in \mathbb{X}$$
2. (Maximum entropy): 讓$\mathbb{X}’ = {x \in \mathbb{X}, P(x) > 0} \subseteq \mathbb{X}$, 可以得到 $$H(X) – log|\mathbb{X}| \leq H(X) – log|\mathbb{X}’| = -\sum_{x \in \mathbb{X}}P(x) \cdot logP(x) – log|\mathbb{X}’| \\ = -\sum_{x \in \mathbb{X}’} P(x) \cdot logP(x) – log|\mathbb{X}’| \cdot\sum_{x \in \mathbb{X}’}P(x) \\ = \sum_{x \in \mathbb{X}’} P(x) \cdot log\frac{1}{P(x)\cdot |\mathbb{X}’|} = log_{2}e \cdot \sum_{x \in \mathbb{X}’}P(x)ln\frac{1}{P(x)\cdot |\mathbb{X}’|} \\ \leq log_{2}e\sum_{x \in \mathbb{X}’}P(x)\cdot(\frac{1}{P(x)\cdot|\mathbb{X}’|}-1) \\ =log_{2}e(\sum_{x \in \mathbb{X}’}\frac{1}{|\mathbb{X}’|} – \sum_{x \in \mathbb{X}’}P(x) = 0$$

等式成立若且唯若

1. $\mathbb{X}’ = \mathbb{X}$, i.e., $P(x) > 0 \> \forall x \in \mathbb{X}$
2. $\frac{1}{P(x)|\mathbb{X}’|} = 1 \Rightarrow P(x) = \frac{1}{|\mathbb{X}’|} \> \forall x \in \mathbb{X}’$
   i.e., $P(x) = \frac{1}{|\mathbb{X}|} \> \forall \> x \in \mathbb{X}$