目錄
自然對數Function
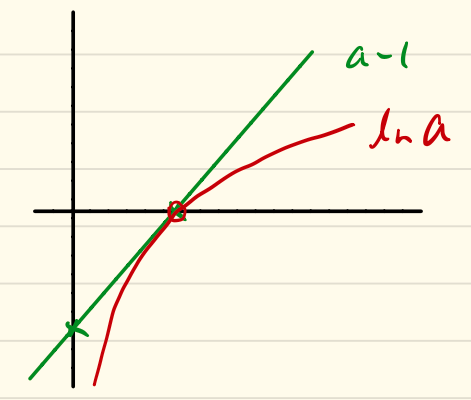
自然對數的fundamental inequality可以定義成:
定理:對於任意的\(a>0, ln a \leq a-1\)等式能夠保持在這個條件之下若且唯若 \(a = 1\)
隨機變數
假設一個\(X\)是Discrete Random Variable(R.V.)遵照alphabet \(\mathbb{X}\) 並且這個\(\mathbb{X}\)屬於Probability Mass Function (PMF),我們可以表示成
\[ P_{X}(x) = Pr{X = x}, x \in \mathbb{X} \]
\(X\)為R.V., \(x\)為實數屬於\(\mathbb{X}\)這個alphabet,而為了方便起見,我們通常表示\(P_{X}(x)\)是\(P(x)\),所以看到\(P(y)\)表示這是屬於另一個\(Y\)的R.V.,故\(P_{X}(x)\)跟\(P_{Y}(y)\)是來自兩個不同的PMF。



